
Stieltjes polynomial
Encyclopedia
In mathematics, the Heine–Stieltjes polynomials or Stieltjes polynomials, introduced by , are polynomial solutions of a second-order Fuchsian equation, a differential equation
all of whose singularities are regular. The Fuchsian equation has the form
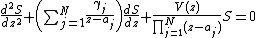
for some polynomial V(z) of degree at most N − 2, and if this has a polynomial solution S then V is called a Van Vleck polynomial (after Edward Burr Van Vleck
) and S is called a Heine–Stieltjes polynomial.
Heun polynomials are the special cases of Stieltjes polynomials when the differential equation has four singular points.
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
all of whose singularities are regular. The Fuchsian equation has the form
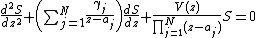
for some polynomial V(z) of degree at most N − 2, and if this has a polynomial solution S then V is called a Van Vleck polynomial (after Edward Burr Van Vleck
Edward Burr Van Vleck
Edward Burr Van Vleck was an American mathematician.The son of astronomer John Monroe Van Vleck, he graduated from Wesleyan University in 1884, attended Johns Hopkins in 1885-87, and studied at Göttingen...
) and S is called a Heine–Stieltjes polynomial.
Heun polynomials are the special cases of Stieltjes polynomials when the differential equation has four singular points.

