
Stieltjes moment problem
Encyclopedia
In mathematics
, the Stieltjes moment problem, named after Thomas Joannes Stieltjes
, seeks necessary and sufficient conditions for a sequence { mn, : n = 0, 1, 2, ... } to be of the form
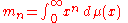
for some measure μ. If such a function μ exists, one asks whether it is unique.
The essential difference between this and other well-known moment problems is that this is on a half-line[ 0, ∞) , whereas in the Hausdorff moment problem one considers a bounded interval [0, 1], and in the Hamburger moment problem one considers the whole line (−∞, ∞).
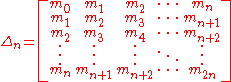
and

Then { mn : n = 1, 2, 3, ... } is a moment sequence of some measure on with infinite support if and only if for all n, both
with infinite support if and only if for all n, both

{ mn : n = 1, 2, 3, ... } is a moment sequence of some measure on with finite support of size m if and only if for all
with finite support of size m if and only if for all  , both
, both

and for all larger

, which states that the solution is unique if

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Stieltjes moment problem, named after Thomas Joannes Stieltjes
Thomas Joannes Stieltjes
Thomas Joannes Stieltjes was a Dutch mathematician. He was born in Zwolle and died in Toulouse, France. He was a pioneer in the field of moment problems and contributed to the study of continued fractions....
, seeks necessary and sufficient conditions for a sequence { mn, : n = 0, 1, 2, ... } to be of the form
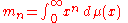
for some measure μ. If such a function μ exists, one asks whether it is unique.
The essential difference between this and other well-known moment problems is that this is on a half-line
Existence
Let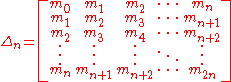
and

Then { mn : n = 1, 2, 3, ... } is a moment sequence of some measure on
 with infinite support if and only if for all n, both
with infinite support if and only if for all n, both
{ mn : n = 1, 2, 3, ... } is a moment sequence of some measure on
 with finite support of size m if and only if for all
with finite support of size m if and only if for all  , both
, both
and for all larger


Uniqueness
There are several sufficient conditions for uniqueness, for example, Carleman's conditionCarleman's condition
In mathematics, Carleman's condition is a sufficient condition for the determinacy of the moment problem.-Hamburger moment problem:For the Hamburger moment problem, the theorem, proved by Torsten Carleman, states the following:...
, which states that the solution is unique if


