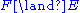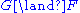
Spider diagram
Encyclopedia
A unitary spider diagram adds existential points to an Euler
or a Venn diagram
. The points indicate the existence of an attribute described by the intersection of contours in the Euler diagram. These points may be joined together forming a shape like a spider
. These represent an OR condition, also known as a logical disjunction
.
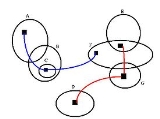
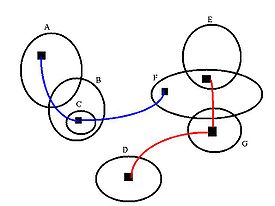In the image shown, the following conjunctions are apparent from the Euler diagram.
The origin of the word spider diagram comes from the word spider. The diagram has many legs just like a spider.
In the universe of discourse defined by this Euler diagram
, in addition to the conjunctions specified above, all possible sets from A through B and D through G are available
separately. The set C is only available as a subset of B. Often, in complicated diagrams, singleton sets and/or conjunctions may be obscured by other set combinations.
The two spiders in the example correspond to the following logical expressions:
Red spider:
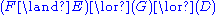
Blue spider:
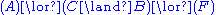
A spider diagram is a unitary spider diagram or the conjunction of two spider diagrams or the disjunction of two spider diagrams or the negation of a spider diagram. That is to say we may form boolean expressions involving unitary spider diagrams and the logical symbols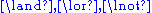
.
The spider diagram logic is expressively equivalent to monadic first order logic with a binary equality relation.
Euler diagram
An Euler diagram is a diagrammatic means of representing sets and their relationships. The first use of "Eulerian circles" is commonly attributed to Swiss mathematician Leonhard Euler . They are closely related to Venn diagrams....
or a Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
. The points indicate the existence of an attribute described by the intersection of contours in the Euler diagram. These points may be joined together forming a shape like a spider
Spider
Spiders are air-breathing arthropods that have eight legs, and chelicerae with fangs that inject venom. They are the largest order of arachnids and rank seventh in total species diversity among all other groups of organisms...
. These represent an OR condition, also known as a logical disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
.
The origin of the word spider diagram comes from the word spider. The diagram has many legs just like a spider.
In the universe of discourse defined by this Euler diagram
Euler diagram
An Euler diagram is a diagrammatic means of representing sets and their relationships. The first use of "Eulerian circles" is commonly attributed to Swiss mathematician Leonhard Euler . They are closely related to Venn diagrams....
, in addition to the conjunctions specified above, all possible sets from A through B and D through G are available
separately. The set C is only available as a subset of B. Often, in complicated diagrams, singleton sets and/or conjunctions may be obscured by other set combinations.
The two spiders in the example correspond to the following logical expressions:
Red spider:
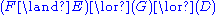
Blue spider:
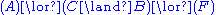
A spider diagram is a unitary spider diagram or the conjunction of two spider diagrams or the disjunction of two spider diagrams or the negation of a spider diagram. That is to say we may form boolean expressions involving unitary spider diagrams and the logical symbols
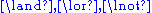.The spider diagram logic is expressively equivalent to monadic first order logic with a binary equality relation.