
Sommerfeld expansion
Encyclopedia
A Sommerfeld expansion is an approximation method developed by Arnold Sommerfeld
for a certain class of integrals which are common in condensed matter and statistical physics. Physically, the integrals represent statistical averages using the Fermi–Dirac distribution.
When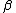 is a large quantity, it can be shown that
is a large quantity, it can be shown that
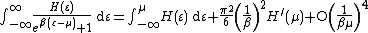
where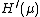 is used to denote the derivative of
is used to denote the derivative of 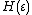 evaluated at
evaluated at 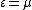 and we have used Big-O notation to describe the approximation's limiting behaviour. The expansion is only valid if
and we have used Big-O notation to describe the approximation's limiting behaviour. The expansion is only valid if  vanishes as
vanishes as  and goes no faster than polynomially in
and goes no faster than polynomially in  as
as 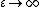 .
.
of solids. In these calculations the above integral expresses the expected value of the quantity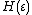 . For these integrals we can then identify
. For these integrals we can then identify 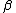 as the inverse temperature and
as the inverse temperature and 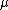 as the chemical potential
as the chemical potential
. Therefore, the Sommerfeld expansion is valid for large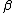 (low temperature
(low temperature
) systems.
Arnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
for a certain class of integrals which are common in condensed matter and statistical physics. Physically, the integrals represent statistical averages using the Fermi–Dirac distribution.
When
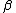 is a large quantity, it can be shown that
is a large quantity, it can be shown that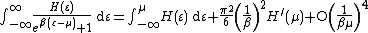
where
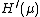 is used to denote the derivative of
is used to denote the derivative of 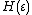 evaluated at
evaluated at 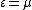 and we have used Big-O notation to describe the approximation's limiting behaviour. The expansion is only valid if
and we have used Big-O notation to describe the approximation's limiting behaviour. The expansion is only valid if  vanishes as
vanishes as  and goes no faster than polynomially in
and goes no faster than polynomially in  as
as 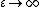 .
.Application to the free electron model
Integrals of this type appear frequently when calculating electronic properties in the free electron modelFree electron model
In solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
of solids. In these calculations the above integral expresses the expected value of the quantity
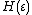 . For these integrals we can then identify
. For these integrals we can then identify 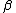 as the inverse temperature and
as the inverse temperature and 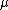 as the chemical potential
as the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
. Therefore, the Sommerfeld expansion is valid for large
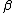 (low temperature
(low temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
) systems.

