
Sobol sequence
Encyclopedia
Sobol sequences are an example of quasi-random low-discrepancy sequence
s. They were first introduced by I.M.Sobol'In Cyrillic as "Илья Меерович Соболь", as per http://www.librarything.com/author/sobolilyam. in 1967.
These sequences use a base of two to form successively finer uniform partitions of the unit interval, and then reorder the coordinates in each dimension.
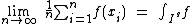
and the convergence be as fast as possible.
It is more or less clear that for the sum to converge towards the integral, the points xn should fill Is minimizing the holes. Another good property would be that the projections of xn on a lower-dimensional face of Is leave very few holes as well. Hence the homogeneous filling of Is does not qualify ; because in lower-dimensions many points will be at the same place, therefore useless for the integral estimation.
These good distributions are called (t,m,s)-nets and (t,s)-sequences in base b. To introduce them, define first an elementary s-interval in base b a subset of Is of the form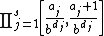 , where aj, dj are integers and aj
, where aj, dj are integers and ajj for all j in {1, ...,s}
Given 2 integers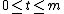 , a (t,m,s)-net in base b is a sequence xn of bm points of Is such that
, a (t,m,s)-net in base b is a sequence xn of bm points of Is such that 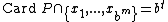 for all elementary interval P in base b of hypervolume λ(P) = bt-m.
for all elementary interval P in base b of hypervolume λ(P) = bt-m.
Given a non-negative integer t, a (t,s)-sequence in base b is an infinite sequence of points xn such that for all integers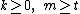 , the sequence
, the sequence 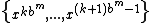 is a (t,m,s)-net in base b.
is a (t,m,s)-net in base b.
In his article, Sobol' spoke of Πτ-meshes and LPτ sequences, which are (t,m,s)-nets and (t,s)-sequences in base 2 respectively. The terms (t,m,s)-nets and (t,s)-sequences in base b (also called Niederreiter sequences) where coined in 1988 by H. Niederreiter. The term Sobol sequences was introduced in late English-speaking papers in comparison with Halton, Faure and other low-discrepancy sequences.
To generate the j-th component of the points in a Sobol' sequence, we need to choose a primitive polynomial
of some degree sj over the field GF(2)
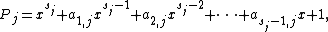
where the coefficients a1,j, a2,j, ..., asj−1,j are either 0 or 1. The error bounds for Sobol' sequences given in indicate that we should use primitive polynomials of as low a degree as possible.
A sequence of positive integers {m1,j, m2,j, ...} are defined by the recurrence relation
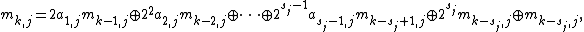
where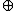 is the bit-by-bit exclusive-or operator. The initial values m1,j, m2,j, ..., msj,j can be chosen freely provided that each mk,j, 1 ≤ k ≤ sj, is odd and less than 2k.
is the bit-by-bit exclusive-or operator. The initial values m1,j, m2,j, ..., msj,j can be chosen freely provided that each mk,j, 1 ≤ k ≤ sj, is odd and less than 2k.
The so-called direction numbers {v1,j, v2,j, . . .}In some papers numbers mk,j also can be referred as direction numbers. are defined by
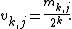
Then xi,j , the j-th component of the i-th point in a Sobol' sequence, is given by
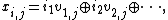
where ik is the k-th binary digit of i = (. . . i3i2i1)2. Here the notation (·)2 denotes the binary representation of numbers.
implementation was proposed by Antonov and Saleev
As for the generation of Sobol' numbers, they are clearly aided by the use of Gray code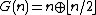 instead of n for constructing the n-th point draw.
instead of n for constructing the n-th point draw.
Suppose we have already generated all the Sobol' sequence draws up to n − 1, and kept in memory the values xn−1,j for all the required dimensions. Since the Gray code G(n) differs from that of the preceding one G(n − 1) by just a single, say the k-th, bit (which is a rightmost bit of n − 1), all that needs to be done is a single XOR operation for each dimension in order to propagate all of the xn−1 to xn, i.e.
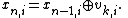
Definition. A low-discrepancy sequence is said to satisfy Property A if for any binary segment (not an arbitrary subset) of the d-dimensional sequence of length 2d there is exactly one draw in each 2d hypercubes that result from subdividing the unit hypercube along each of its length extensions into half.
Definition. A low-discrepancy sequence is said to satisfy Property A’ if for any binary segment (not an arbitrary subset) of the d-dimensional sequence of length 4d there is exactly one draw in each 4d hypercubes that result from subdividing the unit hypercube along each of its length extensions into four equal parts.
There are mathematical conditions that guarantee properties A and A'.
Theorem. The d-dimensional Sobol sequence possesses Property A iff
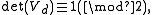
where Vd is the d × d binary matrix defined by
 ,
,
with vk,j,m denoting the m-th digit after the binary point of the direction number vk,j = (0.vk,j,1vk,j,2 . . .)2.
Theorem. The d-dimensional Sobol sequence possesses Property A' iff
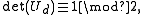
where Ud is the 2d × 2d binary matrix defined by
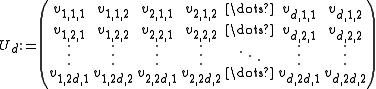 ,
,
with vk,j,m denoting the m-th digit after the binary point of the direction number vk,j = (0.vk,j,1vk,j,2 . . .)2.
Tests for properties A and A’ are independent. Thus it is possible to construct the Sobol’ sequence which satisfies both properties A and A’ or only one of them.
Arguably the easiest choice for the initialisation numbers is just to have the l-th leftmost bit set, and all other bits to be zero, i.e. mk,j = 1 for all k and j. This initialisation is usually called unit initialisation. However, such a sequence fails the test for Property A and A’ even for low dimensions and hence this initialisation is bad.
Good initialisation numbers for different numbers of dimensions are provided by several authors.
Sobol' provides initialisation numbers for dimensions up to 51. The same set of initialisation numbers is used by Bratley and Fox.
Peter Jäckel
provides initialisation numbers up to dimension 32 in his famous book "Monte Carlo methods in finance
".
Other implementations are available as C, Fortran 77, or Fortran 90 routines in the popular Numerical Recipes collection of software (for example, see Press et al.).
Initialisation numbers for high dimensions are available on Joe and Kuo.
There are also some commercial Sobol' sequence generators available, for example see or.
Low-discrepancy sequence
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy....
s. They were first introduced by I.M.Sobol'In Cyrillic as "Илья Меерович Соболь", as per http://www.librarything.com/author/sobolilyam. in 1967.
These sequences use a base of two to form successively finer uniform partitions of the unit interval, and then reorder the coordinates in each dimension.
Good distributions in the s-dimensional unit hypercube
Let Is = [0,1]s be the s-dimensional unit hypercube and f a real integrable function over Is. The original motivation of Sobol' was to construct a sequence xn in Is so that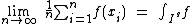
and the convergence be as fast as possible.
It is more or less clear that for the sum to converge towards the integral, the points xn should fill Is minimizing the holes. Another good property would be that the projections of xn on a lower-dimensional face of Is leave very few holes as well. Hence the homogeneous filling of Is does not qualify ; because in lower-dimensions many points will be at the same place, therefore useless for the integral estimation.
These good distributions are called (t,m,s)-nets and (t,s)-sequences in base b. To introduce them, define first an elementary s-interval in base b a subset of Is of the form
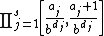 , where aj, dj are integers and aj
, where aj, dj are integers and ajGiven 2 integers
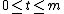 , a (t,m,s)-net in base b is a sequence xn of bm points of Is such that
, a (t,m,s)-net in base b is a sequence xn of bm points of Is such that 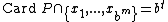 for all elementary interval P in base b of hypervolume λ(P) = bt-m.
for all elementary interval P in base b of hypervolume λ(P) = bt-m.Given a non-negative integer t, a (t,s)-sequence in base b is an infinite sequence of points xn such that for all integers
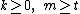 , the sequence
, the sequence 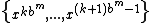 is a (t,m,s)-net in base b.
is a (t,m,s)-net in base b.In his article, Sobol' spoke of Πτ-meshes and LPτ sequences, which are (t,m,s)-nets and (t,s)-sequences in base 2 respectively. The terms (t,m,s)-nets and (t,s)-sequences in base b (also called Niederreiter sequences) where coined in 1988 by H. Niederreiter. The term Sobol sequences was introduced in late English-speaking papers in comparison with Halton, Faure and other low-discrepancy sequences.
Construction of the Sobol sequence
The algorithm for generating Sobol sequences is clearly explained in Bratley and Fox, Algorithm 659To generate the j-th component of the points in a Sobol' sequence, we need to choose a primitive polynomial
Primitive polynomial
In field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
of some degree sj over the field GF(2)
GF(2)
GF is the Galois field of two elements. It is the smallest finite field.- Definition :The two elements are nearly always called 0 and 1, being the additive and multiplicative identities, respectively...
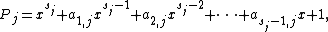
where the coefficients a1,j, a2,j, ..., asj−1,j are either 0 or 1. The error bounds for Sobol' sequences given in indicate that we should use primitive polynomials of as low a degree as possible.
A sequence of positive integers {m1,j, m2,j, ...} are defined by the recurrence relation
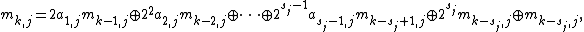
where
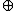 is the bit-by-bit exclusive-or operator. The initial values m1,j, m2,j, ..., msj,j can be chosen freely provided that each mk,j, 1 ≤ k ≤ sj, is odd and less than 2k.
is the bit-by-bit exclusive-or operator. The initial values m1,j, m2,j, ..., msj,j can be chosen freely provided that each mk,j, 1 ≤ k ≤ sj, is odd and less than 2k.The so-called direction numbers {v1,j, v2,j, . . .}In some papers numbers mk,j also can be referred as direction numbers. are defined by
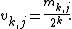
Then xi,j , the j-th component of the i-th point in a Sobol' sequence, is given by
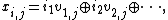
where ik is the k-th binary digit of i = (. . . i3i2i1)2. Here the notation (·)2 denotes the binary representation of numbers.
A fast algorithm for the construction of Sobol sequences
A more efficient Gray codeGray code
The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....
implementation was proposed by Antonov and Saleev
As for the generation of Sobol' numbers, they are clearly aided by the use of Gray code
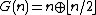 instead of n for constructing the n-th point draw.
instead of n for constructing the n-th point draw.Suppose we have already generated all the Sobol' sequence draws up to n − 1, and kept in memory the values xn−1,j for all the required dimensions. Since the Gray code G(n) differs from that of the preceding one G(n − 1) by just a single, say the k-th, bit (which is a rightmost bit of n − 1), all that needs to be done is a single XOR operation for each dimension in order to propagate all of the xn−1 to xn, i.e.
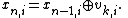
Additional uniformity properties
Sobol’ introduced additional uniformity conditions known as property A and A’.Definition. A low-discrepancy sequence is said to satisfy Property A if for any binary segment (not an arbitrary subset) of the d-dimensional sequence of length 2d there is exactly one draw in each 2d hypercubes that result from subdividing the unit hypercube along each of its length extensions into half.
Definition. A low-discrepancy sequence is said to satisfy Property A’ if for any binary segment (not an arbitrary subset) of the d-dimensional sequence of length 4d there is exactly one draw in each 4d hypercubes that result from subdividing the unit hypercube along each of its length extensions into four equal parts.
There are mathematical conditions that guarantee properties A and A'.
Theorem. The d-dimensional Sobol sequence possesses Property A iff
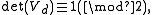
where Vd is the d × d binary matrix defined by
 ,
,with vk,j,m denoting the m-th digit after the binary point of the direction number vk,j = (0.vk,j,1vk,j,2 . . .)2.
Theorem. The d-dimensional Sobol sequence possesses Property A' iff
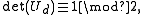
where Ud is the 2d × 2d binary matrix defined by
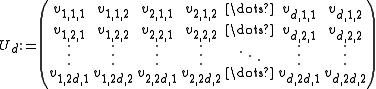 ,
,with vk,j,m denoting the m-th digit after the binary point of the direction number vk,j = (0.vk,j,1vk,j,2 . . .)2.
Tests for properties A and A’ are independent. Thus it is possible to construct the Sobol’ sequence which satisfies both properties A and A’ or only one of them.
The initialization of Sobol' numbers
To construct a Sobol' sequence a set of direction numbers vi,j needs to be selected. There is some freedom in the selection of initial direction numbers.These numbers are usually called initialisation numbers Therefore, it is possible to receive different realisations of the Sobol' sequence for selected dimensions. A bad selection of initial numbers can considerably reduce the efficiency of Sobol sequences when used for computation.Arguably the easiest choice for the initialisation numbers is just to have the l-th leftmost bit set, and all other bits to be zero, i.e. mk,j = 1 for all k and j. This initialisation is usually called unit initialisation. However, such a sequence fails the test for Property A and A’ even for low dimensions and hence this initialisation is bad.
Good initialisation numbers for different numbers of dimensions are provided by several authors.
Sobol' provides initialisation numbers for dimensions up to 51. The same set of initialisation numbers is used by Bratley and Fox.
Peter Jäckel
Peter Jaeckel
Peter Jaeckel is a mathematician who has influenced the development of the use of Monte Carlo methods in Mathematical Finance. Dr. Jaeckel has served as Global Head of Credit, Hybrid, Inflation, and Commodity Derivative Analytics at ABN Amro and has made important contributions in the field of...
provides initialisation numbers up to dimension 32 in his famous book "Monte Carlo methods in finance
Monte Carlo methods in finance
Monte Carlo methods are used in finance and mathematical finance to value and analyze instruments, portfolios and investments by simulating the various sources of uncertainty affecting their value, and then determining their average value over the range of resultant outcomes. This is usually done...
".
Other implementations are available as C, Fortran 77, or Fortran 90 routines in the popular Numerical Recipes collection of software (for example, see Press et al.).
Initialisation numbers for high dimensions are available on Joe and Kuo.
There are also some commercial Sobol' sequence generators available, for example see or.
External links
- Collected Algorithms of the ACM (See algorithms 647, 659, and 738.)
- Collection of Sobol sequences generator programming codes

