
Slutsky's theorem
Encyclopedia
In probability theory
, Slutsky’s theorem extends some properties of algebraic operations on convergent sequences
of real number
s to sequences of random variable
s.
The theorem was named after Eugen Slutsky
. Slutsky’s theorem is also attributed to Harald Cramér
.
s. If Xn converges in distribution to a random element X, and Yn converges in probability to a constant c, then
where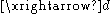 denotes convergence in distribution.
denotes convergence in distribution.
Notes:
Next we apply the continuous mapping theorem
, recognizing the functions g(x,y)=x+y, g(x,y)=xy, and g(x,y)=x−1y as continuous (for the last function to be continuous, x has to be invertible).
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Slutsky’s theorem extends some properties of algebraic operations on convergent sequences
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s to sequences of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s.
The theorem was named after Eugen Slutsky
Eugen Slutsky
Evgeny "Eugen" Evgenievich Slutsky was a Russian/Soviet mathematical statistician, economist and political economist.-Slutsky's work in economics:...
. Slutsky’s theorem is also attributed to Harald Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
.
Statement
Let {Xn}, {Yn} be sequences of scalar/vector/matrix random elementRandom element
In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...
s. If Xn converges in distribution to a random element X, and Yn converges in probability to a constant c, then
-

-

-
 provided that c is invertible,
provided that c is invertible,
where
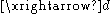 denotes convergence in distribution.
denotes convergence in distribution.Notes:
- In the statement of the theorem, the condition “Yn converges in probability to a constant c” may be replaced with “Yn converges in distribution to a constant c” — these two requirements are equivalent according to this property.
- The requirement that Yn converges to a constant is important — if it were to converge to a non-degenerate random variable, the theorem would be no longer valid.
- The theorem remains valid if we replace all convergences in distribution with convergences in probability (due to this property).
Proof
This theorem follows from the fact that if Xn converges in distribution to X and Yn converges in probability to a constant c, then the joint vector (Xn, Yn) converges in distribution to (X, c) (see here).Next we apply the continuous mapping theorem
Continuous mapping theorem
In probability theory, the continuous mapping theorem states that continuous functions are limit-preserving even if their arguments are sequences of random variables. A continuous function, in Heine’s definition, is such a function that maps convergent sequences into convergent sequences: if xn → x...
, recognizing the functions g(x,y)=x+y, g(x,y)=xy, and g(x,y)=x−1y as continuous (for the last function to be continuous, x has to be invertible).

