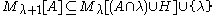Not to be confused with Silver Machines.

In set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, Silver machines are devices used for bypassing the use of fine structure in proofs of statements holding in L

Statements true in L

Here is a list of propositions that hold in the constructible universe :* The generalized continuum hypothesis and as a consequence** The axiom of choice* Diamondsuit** Clubsuit* Global square* The existence of morasses...

. They were invented by set theorist Jack Silver

Jack Silver

Jack Howard Silver is a set theorist and logician at the University of California, Berkeley. He has made several deep contributions to set theory...

 as a means of proving global square holds in the constructible universe

Constructible universe

In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...

.

Preliminaries

An ordinal

Ordinal

Ordinal may refer to:* Ordinal number , a word representing the rank of a number* Ordinal scale, ranking things that are not necessarily numbers* Ordinal indicator, the sign adjacent to a numeral denoting that it is an ordinal number...

is *definable from a class of ordinals X if and only if there is a formula 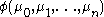and 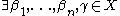such that is the unique ordinal for which where for all we define to be the name for within .

A structure is eligible if and only if:

1. .
2. < is the ordering on On restricted to X.
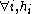3. is a partial function from to X, for some integer k(i).

If is an eligible structure then 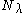is defined to be as before but with all occurrences of X replaced with .

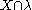Let 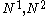be two eligible structures which have the same function k. Then we say if and 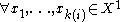we have:

Silver machine

A Silver machine is an eligible structure of the form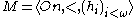 which satisfies the following conditions:

Condensation principle. If then there is an such that .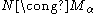

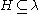Finiteness principle. For each there is a finite set such that for any set we have

Skolem property. If is *definable from the set , then ; moreover there is an ordinal , uniformly 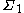definable from , such that .