Siegel-Walfisz theorem
Encyclopedia
In analytic number theory
, the Siegel–Walfisz theorem was obtained by Arnold Walfisz
as an application of a theorem
by Carl Ludwig Siegel
to primes in arithmetic progression
s.
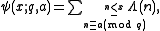
where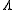
denotes the von Mangoldt function
and φ is Euler's totient function
.
Then the theorem states that given any real number N there exists a positive constant CN depending only on N such that
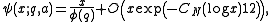
whenever (a, q) = 1 and
because Siegel's theorem is ineffective.
From the theorem we can deduce the following form of the prime number theorem for arithmetic progressions: If, for (a,q)=1, by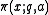
we denote the number of primes less than or equal to x which are congruent to a mod q, then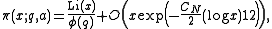
where N, a, q, CN and φ are as in the theorem, and Li denotes the offset logarithmic integral.
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, the Siegel–Walfisz theorem was obtained by Arnold Walfisz
Arnold Walfisz
Arnold Walfisz was a Polish mathematician working in analytic number theory.- Life :After the Abitur in Warsaw Arnold Walfisz studied in Munich, Berlin, Heidelberg and Göttingen. Edmund Landau was his doctoral thesis supervisor at the University of Göttingen...
as an application of a theorem
Siegel zero
In mathematics, more specifically in the field of analytic number theory, a Siegel zero, named after Carl Ludwig Siegel, is a type of potential counterexample to the generalized Riemann hypothesis, on the zeroes of Dirichlet L-function....
by Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
to primes in arithmetic progression
Primes in arithmetic progression
In number theory, the phrase primes in arithmetic progression refers to at least three prime numbers that are consecutive terms in an arithmetic progression, for example the primes ....
s.
Statement of the Siegel–Walfisz theorem
Define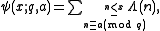where
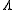denotes the von Mangoldt functionVon Mangoldt function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
and φ is Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
.
Then the theorem states that given any real number N there exists a positive constant CN depending only on N such that
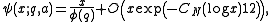
whenever (a, q) = 1 and
Remarks
The constant CN is not effectively computableEffective results in number theory
For historical reasons and in order to have application to the solution of Diophantine equations, results in number theory have been scrutinised more than in other branches of mathematics to see if their content is effectively computable...
because Siegel's theorem is ineffective.
From the theorem we can deduce the following form of the prime number theorem for arithmetic progressions: If, for (a,q)=1, by
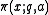we denote the number of primes less than or equal to x which are congruent to a mod q, then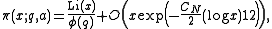where N, a, q, CN and φ are as in the theorem, and Li denotes the offset logarithmic integral.