Shortest common supersequence
Encyclopedia
This shortest common supersequence problem is closely related to the longest common subsequence problem
. Given two sequences X = < x1,...,xm > and Y = < y1,...,yn >, a sequence U = < u1,...,uk > is a common supersequence of X and Y if U is a supersequence of both X and Y. In other words, the shortest common supersequence between strings x and y is the shortest string z such that both x and y are subsequences
of z.
The shortest common supersequence (scs) is a common supersequence of minimal length. In the shortest common supersequence problem, the two sequences X and Y are given and the task is to find a shortest possible common supersequence of these sequences. In general, the scs is not unique.
For two input sequences, an scs can be formed from an lcs easily. For example, if X
and Y
, the lcs is Z
. By inserting the non-lcs symbols while preserving the symbol order, we get the scs: U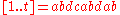
.
It is quite clear that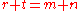
for two input sequences. However, for three or more input sequences this does not hold. Note also, that the lcs and the scs problems are not dual problems
.
Longest common subsequence problem
The longest common subsequence problem is to find the longest subsequence common to all sequences in a set of sequences . Note that subsequence is different from a substring, see substring vs. subsequence...
. Given two sequences X = < x1,...,xm > and Y = < y1,...,yn >, a sequence U = < u1,...,uk > is a common supersequence of X and Y if U is a supersequence of both X and Y. In other words, the shortest common supersequence between strings x and y is the shortest string z such that both x and y are subsequences
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
of z.
The shortest common supersequence (scs) is a common supersequence of minimal length. In the shortest common supersequence problem, the two sequences X and Y are given and the task is to find a shortest possible common supersequence of these sequences. In general, the scs is not unique.
For two input sequences, an scs can be formed from an lcs easily. For example, if X
and Y, the lcs is Z. By inserting the non-lcs symbols while preserving the symbol order, we get the scs: U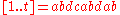.It is quite clear that
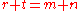for two input sequences. However, for three or more input sequences this does not hold. Note also, that the lcs and the scs problems are not dual problemsDual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
.