
Shephard's problem
Encyclopedia
In mathematics
, Shephard's problem, is the following geometrical question asked by : if K and L are centrally symmetric convex bodies
in n-dimension
al Euclidean space
such that whenever K and L are projected
onto a hyperplane
, the volume
of the projection of K is smaller than the volume of the projection of L, then does it follow that the volume of K is smaller than that of L?
In this case, "centrally symmetric" means that the reflection of K in the origin, −K, is a translate of K, and similarly for L. If πk : Rn → Πk is a projection of Rn onto some k-dimensional hyperplane Πk (not necessarily a coordinate hyperplane) and Vk denotes k-dimensional volume, Shephard's problem is to determine the truth or falsity of the implication
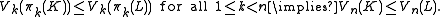
Vk(πk(K)) is sometimes known as the brightness of K and the function Vk o πk as a (k-dimensional) brightness function.
In dimensions n = 1 and 2, the answer to Shephard's problem is "yes". In 1967, however, Petty and Schneider showed that the answer is "no" for every n ≥ 3. The solution of Shephard's problem requires Minkowski's first inequality for convex bodies
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Shephard's problem, is the following geometrical question asked by : if K and L are centrally symmetric convex bodies
Convex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
in n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
such that whenever K and L are projected
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
onto a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
, the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of the projection of K is smaller than the volume of the projection of L, then does it follow that the volume of K is smaller than that of L?
In this case, "centrally symmetric" means that the reflection of K in the origin, −K, is a translate of K, and similarly for L. If πk : Rn → Πk is a projection of Rn onto some k-dimensional hyperplane Πk (not necessarily a coordinate hyperplane) and Vk denotes k-dimensional volume, Shephard's problem is to determine the truth or falsity of the implication
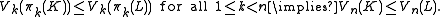
Vk(πk(K)) is sometimes known as the brightness of K and the function Vk o πk as a (k-dimensional) brightness function.
In dimensions n = 1 and 2, the answer to Shephard's problem is "yes". In 1967, however, Petty and Schneider showed that the answer is "no" for every n ≥ 3. The solution of Shephard's problem requires Minkowski's first inequality for convex bodies
Minkowski's first inequality for convex bodies
In mathematics, Minkowski's first inequality for convex bodies is a geometrical result due to the German mathematician Hermann Minkowski. The inequality is closely related to the Brunn–Minkowski inequality and the isoperimetric inequality....
.

