Shelling (topology)
Encyclopedia
In mathematics
, a shelling of a simplicial complex
is a way of gluing it together from its maximal simplices in a well-behaved way. A complex admitting a shelling is called shellable.
be a finite or countably infinite simplicial complex. An ordering 
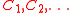of the maximal simplices of 
is a shelling if the complex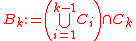 
is pure and 
-dimensional for all 
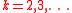. If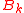 
is the entire boundary of 
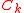then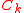 
is called spanning.
For
not necessarily countable, one can define a shelling as a well-ordering of the maximal simplices of 
having analogous properties.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a shelling of a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
is a way of gluing it together from its maximal simplices in a well-behaved way. A complex admitting a shelling is called shellable.
Definition
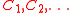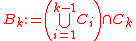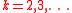A d-dimensional simplicial complex is called pure if its maximal simplices all have dimension d. Let be a finite or countably infinite simplicial complex. An ordering of the maximal simplices of is a shelling if the complex is pure and -dimensional for all . If 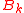is the entire boundary of 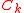then 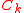is called spanning.For
not necessarily countable, one can define a shelling as a well-ordering of the maximal simplices of having analogous properties.Properties
- A shellable complex is homotopy equivalentHomotopyIn topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
to a wedge sumWedge sumIn topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of spheres, one for each spanning simplex and of corresponding dimension. - A shellable complex may admit many different shellings, but the number of spanning simplices, and their dimensions, do not depend on the choice of shelling. This follows from the previous property.
Examples
- Every Coxeter complex, and more generally every building, is shellable.