Shanks' square forms factorization
Encyclopedia
Shanks' square forms factorization is a method for integer factorization
devised by Daniel Shanks
as an improvement on Fermat's factorization method
.
The success of Fermat's method depends on finding integers
and 
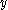such that 
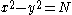, where 
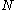is the integer to be factored. An improvement (noticed by Kraitchik
) is to look for integers
and 
such that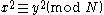 
. Finding a suitable pair 
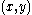does not guarantee a factorization of 
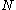, but it implies that 
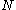is a factor of 
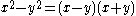, and there is a good chance that the prime divisors of 
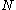are distributed between these two factors, so that calculation of the greatest common divisor
of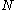
and 
will give a non-trivial factor of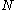 
.
A practical algorithm for finding pairs
which satisfy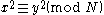 
was developed by Shanks, who named it Square Forms Factorization or SQUFOF. The algorithm can be expressed in terms of continued fractions, or in terms of quadratic forms. Although there are now much more efficient factorization methods available, SQUFOF has the advantage that it is small enough to be implemented on a programmable calculator.
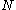, the integer to be factored, which must be neither a prime number
nor a perfect square
, and a small multiplier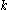
.
Output: a non-trivial factor of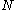
.
The algorithm:
Initialize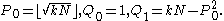
Repeat
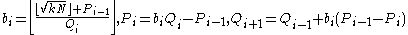
until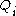
is a perfect square.
Initialize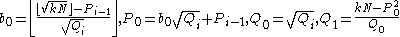
Repeat
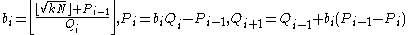
until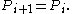
Then if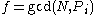
is not equal to 
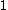and not equal to 
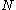, then 
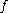is a non-trivial factor of 
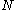. Otherwise try another value of 
.
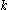Shanks' method has time complexity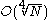
.
Stephen S. McMasters (see link in External Link section) wrote
a more detailed discussion of the mathematics of Shanks' method,
together with a proof of its correctness.
P0 = 105 Q0 = 1 Q1 = 86
P1 = 67 Q1 = 86 Q2 = 77
P2 = 87 Q2 = 77 Q3 = 46
P3 = 97 Q3 = 46 Q4 = 37
P4 = 88 Q4 = 37 Q5 = 91
P5 = 94 Q5 = 91 Q6 = 25
Here Q6 is a perfect square
P0 = 104 Q0 = 5 Q1 = 59
P1 = 73 Q1 = 59 Q2 = 98
P2 = 25 Q2 = 98 Q3 = 107
P3 = 82 Q3 = 107 Q4 = 41
P4 = 82
Here P3 = P4
gcd(11111, 82) = 41, which is a factor of 11111.
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
devised by Daniel Shanks
Daniel Shanks
Daniel Shanks was an American mathematician who worked primarily in numerical analysis and number theory. He is best known as the first to compute π to 100,000 decimal places, and for his book Solved and Unsolved Problems in Number Theory.-Life and education:Dan Shanks was born on January 17,...
as an improvement on Fermat's factorization method
Fermat's factorization method
Fermat's factorization method, named after Pierre de Fermat, is based on the representation of an odd integer as the difference of two squares:N = a^2 - b^2.\...
.
The success of Fermat's method depends on finding integers
and 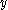such that 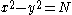, where 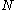is the integer to be factored. An improvement (noticed by KraitchikMaurice Kraitchik
Maurice Kraitchik was a Belgian mathematician and populariser born in Minsk. His main interests were the theory of numbers and recreational mathematics.He is famous for having inspired the two envelopes problem in 1953, with the following puzzle in...
) is to look for integers
and such that 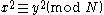. Finding a suitable pair 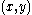does not guarantee a factorization of 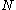, but it implies that 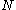is a factor of 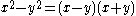, and there is a good chance that the prime divisors of 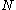are distributed between these two factors, so that calculation of the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of
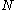and will give a non-trivial factor of 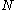.A practical algorithm for finding pairs
which satisfy 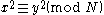was developed by Shanks, who named it Square Forms Factorization or SQUFOF. The algorithm can be expressed in terms of continued fractions, or in terms of quadratic forms. Although there are now much more efficient factorization methods available, SQUFOF has the advantage that it is small enough to be implemented on a programmable calculator.Algorithm
Input: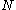, the integer to be factored, which must be neither a prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
nor a perfect square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
, and a small multiplier
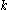.Output: a non-trivial factor of
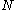.The algorithm:
Initialize
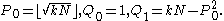
Repeat
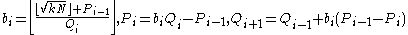
until
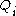is a perfect square.Initialize
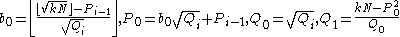
Repeat
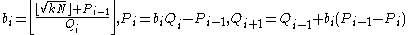
until
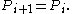
Then if
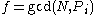is not equal to 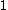and not equal to 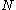, then 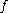is a non-trivial factor of 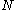. Otherwise try another value of 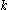.Shanks' method has time complexity
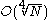.Stephen S. McMasters (see link in External Link section) wrote
a more detailed discussion of the mathematics of Shanks' method,
together with a proof of its correctness.
Example
N = 11111, k = 1P0 = 105 Q0 = 1 Q1 = 86
P1 = 67 Q1 = 86 Q2 = 77
P2 = 87 Q2 = 77 Q3 = 46
P3 = 97 Q3 = 46 Q4 = 37
P4 = 88 Q4 = 37 Q5 = 91
P5 = 94 Q5 = 91 Q6 = 25
Here Q6 is a perfect square
P0 = 104 Q0 = 5 Q1 = 59
P1 = 73 Q1 = 59 Q2 = 98
P2 = 25 Q2 = 98 Q3 = 107
P3 = 82 Q3 = 107 Q4 = 41
P4 = 82
Here P3 = P4
gcd(11111, 82) = 41, which is a factor of 11111.