Secant variety
Encyclopedia
In Algebraic Geometry
, the Zariski closure of the union of the secant line
s to an embedded projective variety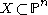
is the first secant variety to 
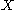. It is usually denoted 
.
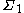The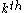
secant variety is the Zariski closure of the union of the linear spaces spanned by collections of k+1 points on 
. It is usually denoted 
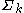. Unless 
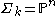, it is always singular along 
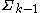, but may have other singular points.
If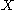
has dimension d, the dimension of 
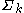is at most kd+d+k.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Zariski closure of the union of the secant line
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
s to an embedded projective variety
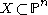is the first secant variety to 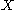. It is usually denoted 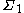.The
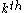secant variety is the Zariski closure of the union of the linear spaces spanned by collections of k+1 points on . It is usually denoted 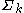. Unless 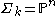, it is always singular along 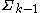, but may have other singular points.If
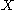has dimension d, the dimension of 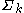is at most kd+d+k.