Scleronomous
Encyclopedia
A mechanical system is scleronomous if the equations of constraints do not contain the time as an explicit variable. Such constraints are called scleronomic constraints.
In 3-D space, a particle with mass , velocity
, velocity  has kinetic energy
has kinetic energy
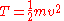 .
.
Velocity is the derivative of position with respect time. Use chain rule for several variables: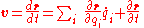 .
.
Therefore,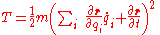 .
.
Rearranging the terms carefully,
 :
: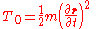 ,
,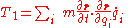 ,
,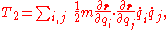 .
.
 ,
, 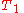 ,
, 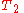 are respectively homogeneous function
are respectively homogeneous function
s of degree 0, 1, and 2 in generalized velocities. If this system is scleronomous, then, the position does not depend explicitly with time:
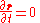 .
.
Therefore, only term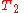 does not vanish:
does not vanish: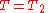 .
.
Kinetic energy is a homogeneous function of degree 2 in generalized velocities .
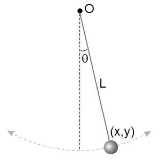
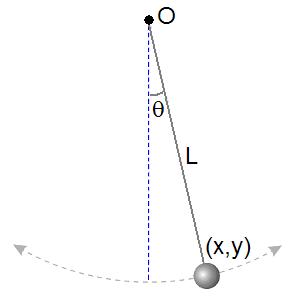 As shown at right, a simple pendulum
As shown at right, a simple pendulum
is a system composed of a weight and a string. The string is attached at the top end to a pivot and at the bottom end to a weight. Being inextensible, the string’s length is a constant. Therefore, this system is scleronomous; it obeys scleronomic constraint
where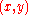 is the position of the weight and
is the position of the weight and 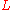 is length of the string.
is length of the string.
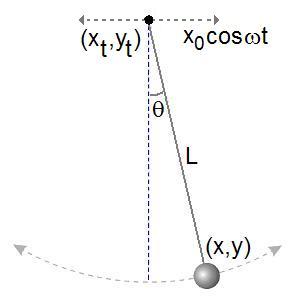 Take a more complicated example. Refer to the next figure at right, Assume the top end of the string is attached to a pivot point undergoing a simple harmonic motion
Take a more complicated example. Refer to the next figure at right, Assume the top end of the string is attached to a pivot point undergoing a simple harmonic motion
 ,
,
where is amplitude,
is amplitude,  is angular frequency, and
is angular frequency, and  is time.
is time.
Although the top end of the string is not fixed, the length of this inextensible string is still a constant. The distance between the top end and the weight must stay the same. Therefore, this system is a rheonomous; it obeys rheonomic constraint .
.
Application
- Main article:Generalized velocity
In 3-D space, a particle with mass
 , velocity
, velocity  has kinetic energy
has kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
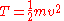 .
.Velocity is the derivative of position with respect time. Use chain rule for several variables:
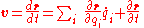 .
.Therefore,
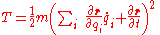 .
.Rearranging the terms carefully,
 :
: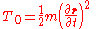 ,
,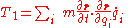 ,
,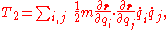 .
. ,
, 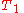 ,
, 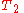 are respectively homogeneous function
are respectively homogeneous functionHomogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
s of degree 0, 1, and 2 in generalized velocities. If this system is scleronomous, then, the position does not depend explicitly with time:
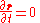 .
.Therefore, only term
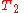 does not vanish:
does not vanish: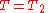 .
.Kinetic energy is a homogeneous function of degree 2 in generalized velocities .
Example: pendulum

Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
is a system composed of a weight and a string. The string is attached at the top end to a pivot and at the bottom end to a weight. Being inextensible, the string’s length is a constant. Therefore, this system is scleronomous; it obeys scleronomic constraint
-
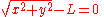 ,
,
where
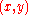 is the position of the weight and
is the position of the weight and 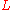 is length of the string.
is length of the string.
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
 ,
,where
 is amplitude,
is amplitude,  is angular frequency, and
is angular frequency, and  is time.
is time.Although the top end of the string is not fixed, the length of this inextensible string is still a constant. The distance between the top end and the weight must stay the same. Therefore, this system is a rheonomous; it obeys rheonomic constraint
 .
.See also
- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
- Holonomic system
- Nonholonomic systemNonholonomic systemA nonholonomic system in physics and mathematics is a system whose state depends on the path taken to achieve it. Such a system is described by a set of parameters subject to differential constraints, such that when the system evolves along a path in its parameter space but finally returns to the...
- RheonomousRheonomousA mechanical system is rheonomous if the equations of constraints contain the time as an explicit variable. Such constraints are called rheonomic constraints.-Example: pendulum:...

