
Schur's theorem
Encyclopedia
In discrete mathematics
, Schur's theorem is either of two different theorems of the mathematician
Issai Schur
. In differential geometry, Schur's theorem is a theorem of A. Schur. In functional analysis
, Schur's theorem is often called Schur's property
, also due to Issai Schur.
, Schur's theorem states that for any partition
of the positive integers into a finite number of parts, one of the parts contains three integers x, y, z with
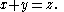
Moreover, for every positive integer c, there exists a number S(c), called Schur's number, such that for every partition of the integers
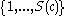
into c parts, one of the parts contains integers x, y, and z with
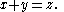
Folkman's theorem
generalizes Schur's theorem by stating that there exist arbitrarily large sets of integers all of whose nonempty sums belong to the same part.
, Schur's theorem tells the number of ways for expressing a given number as a (non-negative, integer) linear combination of a fixed set of relatively prime numbers. In particular, if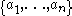 is a set of integers such that
is a set of integers such that 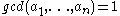 , the number of different tuples of non-negative integer numbers
, the number of different tuples of non-negative integer numbers  such that
such that 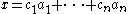 when
when  goes to infinity is:
goes to infinity is:
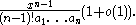
As a result, for every set of relatively prime numbers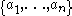 there exists a value of
there exists a value of  such that every larger number is representable as a linear combination of
such that every larger number is representable as a linear combination of 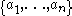 in at least one way. This consequence of the theorem can be recast in a familiar context considering the problem of changing an amount using a set of coins. If the denominations of the coins are relatively prime numbers (such as 2 and 5) then any sufficiently large amount can be changed using only these coins. (See Coin problem
in at least one way. This consequence of the theorem can be recast in a familiar context considering the problem of changing an amount using a set of coins. If the denominations of the coins are relatively prime numbers (such as 2 and 5) then any sufficiently large amount can be changed using only these coins. (See Coin problem
.)
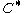 to the distance between the endpoints of a corresponding plane curve
to the distance between the endpoints of a corresponding plane curve 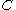 of less curvature.
of less curvature.
Suppose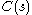 is a plane curve with curvature
is a plane curve with curvature 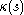 which makes a convex curve when closed by the chord connecting its endpoints, and
which makes a convex curve when closed by the chord connecting its endpoints, and  is a curve of the same length with curvature
is a curve of the same length with curvature 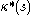 . Let
. Let 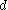 denote the distance between the endpoints of
denote the distance between the endpoints of 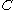 and
and 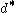 denote the distance between the endpoints of
denote the distance between the endpoints of 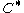 . If
. If 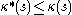 then
then 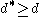 .
.
Schur's theorem is usually stated for curves, but John M. Sullivan has observed that Schur's theorem applies to curves of finite total curvature (the statement is slightly different).
curves, but John M. Sullivan has observed that Schur's theorem applies to curves of finite total curvature (the statement is slightly different).
Schur’s theorem is referred to as either the triangularization of a square matrix with complex entries, or of a square matrix with real entries and real eigenvalues.
and the study of Banach space
s, Schur's theorem, due to J. Schur, often refers to Schur's property
, that for certain spaces, weak convergence
implies convergence in the norm.
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
, Schur's theorem is either of two different theorems of the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
. In differential geometry, Schur's theorem is a theorem of A. Schur. In functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, Schur's theorem is often called Schur's property
Schur's property
In mathematics, Schur's property, named after Issai Schur, is the property of normed spaces that is satisfied precisely if weak convergence of sequences entails convergence in norm.-Motivation:...
, also due to Issai Schur.
Ramsey theory
In Ramsey theoryRamsey theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
, Schur's theorem states that for any partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the positive integers into a finite number of parts, one of the parts contains three integers x, y, z with
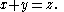
Moreover, for every positive integer c, there exists a number S(c), called Schur's number, such that for every partition of the integers
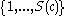
into c parts, one of the parts contains integers x, y, and z with
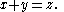
Folkman's theorem
Folkman's theorem
Folkman's theorem is a theorem in mathematics, and more particularly in arithmetic combinatorics and Ramsey theory. According to this theorem, whenever the natural numbers are partitioned into finitely many subsets, there exist arbitrarily large sets of numbers all of whose sums belong to the same...
generalizes Schur's theorem by stating that there exist arbitrarily large sets of integers all of whose nonempty sums belong to the same part.
Combinatorics
In combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, Schur's theorem tells the number of ways for expressing a given number as a (non-negative, integer) linear combination of a fixed set of relatively prime numbers. In particular, if
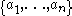 is a set of integers such that
is a set of integers such that 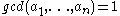 , the number of different tuples of non-negative integer numbers
, the number of different tuples of non-negative integer numbers  such that
such that 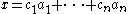 when
when  goes to infinity is:
goes to infinity is: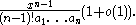
As a result, for every set of relatively prime numbers
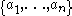 there exists a value of
there exists a value of  such that every larger number is representable as a linear combination of
such that every larger number is representable as a linear combination of 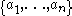 in at least one way. This consequence of the theorem can be recast in a familiar context considering the problem of changing an amount using a set of coins. If the denominations of the coins are relatively prime numbers (such as 2 and 5) then any sufficiently large amount can be changed using only these coins. (See Coin problem
in at least one way. This consequence of the theorem can be recast in a familiar context considering the problem of changing an amount using a set of coins. If the denominations of the coins are relatively prime numbers (such as 2 and 5) then any sufficiently large amount can be changed using only these coins. (See Coin problemCoin problem
The coin problem is a mathematical problem that asks what is the largest monetary amount that cannot be obtained using only coins of specified denominations. For example, the largest amount that cannot be obtained using only coins of 3 and 5 units is 7 units...
.)
Differential geometry
In differential geometry, Schur's theorem compares the distance between the endpoints of a space curve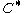 to the distance between the endpoints of a corresponding plane curve
to the distance between the endpoints of a corresponding plane curve 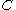 of less curvature.
of less curvature.Suppose
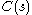 is a plane curve with curvature
is a plane curve with curvature 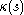 which makes a convex curve when closed by the chord connecting its endpoints, and
which makes a convex curve when closed by the chord connecting its endpoints, and  is a curve of the same length with curvature
is a curve of the same length with curvature 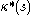 . Let
. Let 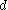 denote the distance between the endpoints of
denote the distance between the endpoints of 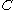 and
and 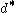 denote the distance between the endpoints of
denote the distance between the endpoints of 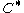 . If
. If 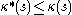 then
then 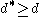 .
.Schur's theorem is usually stated for
 curves, but John M. Sullivan has observed that Schur's theorem applies to curves of finite total curvature (the statement is slightly different).
curves, but John M. Sullivan has observed that Schur's theorem applies to curves of finite total curvature (the statement is slightly different).Linear Algebra
In linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
Schur’s theorem is referred to as either the triangularization of a square matrix with complex entries, or of a square matrix with real entries and real eigenvalues.
Functional analysis
In functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and the study of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, Schur's theorem, due to J. Schur, often refers to Schur's property
Schur's property
In mathematics, Schur's property, named after Issai Schur, is the property of normed spaces that is satisfied precisely if weak convergence of sequences entails convergence in norm.-Motivation:...
, that for certain spaces, weak convergence
Weak convergence
In mathematics, weak convergence may refer to:* The weak convergence of random variables of a probability distribution.* The weak convergence of a sequence of probability measures....
implies convergence in the norm.
Further reading
- Daniel Panario (2005). Integer Partition and The Money Changing Problem.
- Dany Breslauer and Devdatt P. Dubhashi (1995). Combinatorics for Computer Scientists
- John M. Sullivan (2006). Curves of Finite Total Curvature. arXiv.

