
Sazonov's theorem
Encyclopedia
In mathematics
, Sazonov's theorem, named after Vyacheslav Vasilievich Sazonov , is a theorem
in functional analysis
.
It states that a bounded linear operator
between two Hilbert space
s is γ-radonifying if it is Hilbert–Schmidt. The result is also important in the study of stochastic processes and the Malliavin calculus
, since results concerning probability measure
s on infinite-dimensional spaces are of central importance in these fields. Sazonov's theorem also has a converse: if the map is not Hilbert–Schmidt, then it is not γ-radonifying.
from G to H. Recall that T is said to be γ-radonifying if the push forward
of the canonical Gaussian cylinder set measure on G is a bona fide measure
on H. Recall also that T is said to be Hilbert–Schmidt if there is an orthonormal basis
{ ei | i ∈ I } of G such that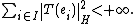
Then Sazonov's theorem is that T is γ-radonifying if it is Hilbert–Schmidt.
The proof uses Prokhorov's theorem
.
on an infinite-dimensional Hilbert space can never be a bona fide measure; equivalently, the identity function
on such a space cannot be γ-radonifying.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Sazonov's theorem, named after Vyacheslav Vasilievich Sazonov , is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
It states that a bounded linear operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
between two Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s is γ-radonifying if it is Hilbert–Schmidt. The result is also important in the study of stochastic processes and the Malliavin calculus
Malliavin calculus
The Malliavin calculus, named after Paul Malliavin, is a theory of variational stochastic calculus. In other words it provides the mechanics to compute derivatives of random variables....
, since results concerning probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s on infinite-dimensional spaces are of central importance in these fields. Sazonov's theorem also has a converse: if the map is not Hilbert–Schmidt, then it is not γ-radonifying.
Statement of the theorem
Let G and H be two Hilbert spaces and let T : G → H be a bounded operatorBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
from G to H. Recall that T is said to be γ-radonifying if the push forward
Pushforward measure
In measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
of the canonical Gaussian cylinder set measure on G is a bona fide measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on H. Recall also that T is said to be Hilbert–Schmidt if there is an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
{ ei | i ∈ I } of G such that
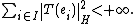
Then Sazonov's theorem is that T is γ-radonifying if it is Hilbert–Schmidt.
The proof uses Prokhorov's theorem
Prokhorov's theorem
In measure theory Prokhorov’s theorem relates tightness of measures to weak compactness in the space of probability measures. It is credited to the Soviet mathematician Yuri Vasilevich Prokhorov, who considered probability measures on complete separable metric spaces...
.
Remarks
The canonical Gaussian cylinder set measureCylinder set measure
In mathematics, cylinder set measure is a kind of prototype for a measure on an infinite-dimensional vector space...
on an infinite-dimensional Hilbert space can never be a bona fide measure; equivalently, the identity function
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on such a space cannot be γ-radonifying.

