S2P (complexity)
Encyclopedia
In computational complexity theory
, S is a complexity class
. A language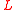
is in 
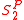if there exists a polynomial-time predicate P such that
where size of y and z must be polynomial of x.
also belongs to S. For by definition, a language L is in NP, if and only if there exists a polynomial-time verifier V(x,y), such that for every x in L there exists y for which V answers true, and such that for every x not in L, V always answers false. But such a verifier can easily be transformed into an S predicate P(x,y,z) for the same language that ignores z and otherwise behaves the same as V.
More strongly, the class S contains MA (a generalization of Sipser–Lautemann theorem) and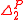
.
By definition, S is contained in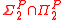
. Futhermore it is contained in ZPPNP.
has polynomial size circuits
then the polynomial time hierarchy collapses to S. This result yields a strengthening of Kannan's theorem: it is known that S is not contained in SIZE(nk) for any fixed k.
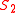as an operator on complexity classes; then 
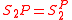. Iteration of 
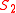operator yields "symmetric hierarchy".
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, S is a complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
. A language
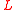is in 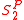if there exists a polynomial-time predicate P such that- If
, then there exists a y such that for all z,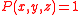 
- If
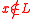, then there exists a z such that for all y,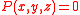 
where size of y and z must be polynomial of x.
Relations to other complexity classes
Every language in NPNP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
also belongs to S. For by definition, a language L is in NP, if and only if there exists a polynomial-time verifier V(x,y), such that for every x in L there exists y for which V answers true, and such that for every x not in L, V always answers false. But such a verifier can easily be transformed into an S predicate P(x,y,z) for the same language that ignores z and otherwise behaves the same as V.
More strongly, the class S contains MA (a generalization of Sipser–Lautemann theorem) and
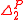.By definition, S is contained in
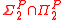. Futhermore it is contained in ZPPNP. Karp–Lipton theorem
A version of Karp–Lipton theorem states that if every language in NPNP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
has polynomial size circuits
P/poly
In computational complexity theory, P/poly is the complexity class of languages recognized by a polynomial-time Turing machine with a polynomial-bounded advice function. It is also equivalently defined as the class PSIZE of languages that have a polynomial-size circuits...
then the polynomial time hierarchy collapses to S. This result yields a strengthening of Kannan's theorem: it is known that S is not contained in SIZE(nk) for any fixed k.
Symmetric hierarchy
As an extension, it is possible to define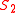 as an operator on complexity classes; then 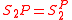. Iteration of 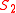operator yields "symmetric hierarchy".External links
- Complexity Class of the Week: S2P, Lance FortnowLance FortnowLance Jeremy Fortnow is a computer scientist in the field of computational complexity and its applications, notable for producing major results on interactive proof systems.-Biography:...
, August 28, 2002.