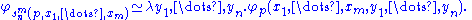S-m-n theorem
Encyclopedia
In computability theory
the smn theorem, (also called the translation lemma, parameter theorem, or parameterization theorem) is a basic result about programming language
s (and, more generally, Gödel numberings of the computable function
s) (Soare 1987, Rogers 1967). It was first proved by Stephen Cole Kleene
(Kleene 1943).
In practical terms, the theorem says that for a given programming language and positive integers m and n, there is a particular algorithm
that operates on the source code
of programs with m + n free variables. This algorithm effectively binds m given values to the first n free variables in the program and leaves the rest free.
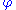of recursive functions, there is a primitive recursive function
s of two arguments with the following property: for every Gödel number p of a partial computable function f with two arguments,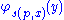
and 
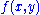are defined for the same combinations of x and y and equal for those combinations. In other words, the following extensional equality of functions holds:
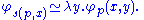
To generalize the theorem, choose a scheme for encoding n numbers as one number, so that the original numbers can be extracted by primitive recursive functions. For example, one might interleave the bit
s of the numbers. Then for any m, n > 0, there exists a primitive recursive function
of m + 1 arguments that behaves as follows: for every Gödel number p of a partial computable function with m + n arguments,
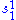is just the function s already described.
code implements s11 for Lisp.
(defun s11 (f x)
(let ((y (gensym)))
(list 'lambda (list y) (list f x y))))
For example, (s11 '(lambda (x y) (+ x y)) 3) evaluates to (lambda (g42) ((lambda (x y) (+ x y)) 3 g42)).
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
the smn theorem, (also called the translation lemma, parameter theorem, or parameterization theorem) is a basic result about programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s (and, more generally, Gödel numberings of the computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s) (Soare 1987, Rogers 1967). It was first proved by Stephen Cole Kleene
Stephen Cole Kleene
Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
(Kleene 1943).
In practical terms, the theorem says that for a given programming language and positive integers m and n, there is a particular algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that operates on the source code
Source code
In computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source...
of programs with m + n free variables. This algorithm effectively binds m given values to the first n free variables in the program and leaves the rest free.
Details
The basic form of the theorem applies to functions of two arguments. Given a Gödel numbering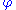 of recursive functions, there is a primitive recursive functionPrimitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
s of two arguments with the following property: for every Gödel number p of a partial computable function f with two arguments,
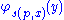and 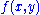are defined for the same combinations of x and y and equal for those combinations. In other words, the following extensional equality of functions holds: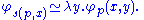To generalize the theorem, choose a scheme for encoding n numbers as one number, so that the original numbers can be extracted by primitive recursive functions. For example, one might interleave the bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s of the numbers. Then for any m, n > 0, there exists a primitive recursive function
of m + 1 arguments that behaves as follows: for every Gödel number p of a partial computable function with m + n arguments,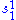
is just the function s already described.Example
The following LispLisp programming language
Lisp is a family of computer programming languages with a long history and a distinctive, fully parenthesized syntax. Originally specified in 1958, Lisp is the second-oldest high-level programming language in widespread use today; only Fortran is older...
code implements s11 for Lisp.
(defun s11 (f x)
(let ((y (gensym)))
(list 'lambda (list y) (list f x y))))
For example, (s11 '(lambda (x y) (+ x y)) 3) evaluates to (lambda (g42) ((lambda (x y) (+ x y)) 3 g42)).