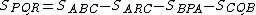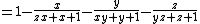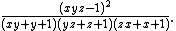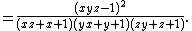In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the intersection of three cevian

Cevian

In geometry, a cevian is any line segment in a triangle with one endpoint on a vertex of the triangle and the other endpoint on the opposite side. Medians, altitudes, and angle bisectors are special cases of cevians...

s. The theorem states that if in triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

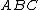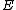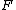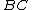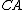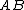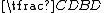
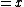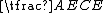
  points , , and lie on segments , , and , then writing , , 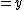and 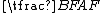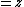, the signed area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

 of the triangle formed by the cevians , , 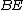and is the area of triangle 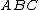times

This theorem was given by Edward John Routh on page 82 of his Treatise on Analytical Statics with Numerous Examples in 1896. The particular case 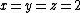has become popularized as the one-seventh area triangle

One-seventh area triangle

In plane geometry, a triangle ABC contains a triangle of one-seventh area of ABC formed as follows: the sides of this triangle lie on lines p, q, r whereA more general result is known as Routh's theorem.-References:...

. The 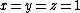case implies that the three median

Median (geometry)

In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...

s are concurrent (through the centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

).

Proof

Suppose the area of triangle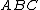 is 1. For triangle 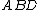and line 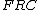using Menelaus's theorem, We could obtain: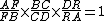

Then

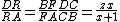
So the are of triangle 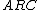is: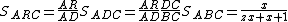

Similarly, we could know: 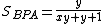and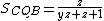

Thus the area of traingle 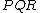is: