
Rotation map
Encyclopedia
In mathematics
, a rotation map is a function that represents an undirected edge-labeled graph, where each vertex enumerates its outgoing neighbors. Rotation maps were first introduced by Reingold, Vadhan and Wigderson (“Entropy waves, the zig-zag graph product, and new constant-degree expanders”, 2002) in order to conveniently define the zig-zag product
and prove its properties.
Given a vertex and an edge label
and an edge label  , the rotation map returns the
, the rotation map returns the  'th neighbor of
'th neighbor of  and the edge label that would lead back to
and the edge label that would lead back to  .
.
 is defined as follows:
is defined as follows: 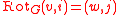 if the ith edge leaving v leads to w, and the jth edge leaving w leads to v.
if the ith edge leaving v leads to w, and the jth edge leaving w leads to v.
 is a permutation, and moreover
is a permutation, and moreover 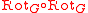 is the identity map.
is the identity map.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a rotation map is a function that represents an undirected edge-labeled graph, where each vertex enumerates its outgoing neighbors. Rotation maps were first introduced by Reingold, Vadhan and Wigderson (“Entropy waves, the zig-zag graph product, and new constant-degree expanders”, 2002) in order to conveniently define the zig-zag product
Zig-zag product
In graph theory, the zig-zag product of regular graphs G,H, denoted by G \circ H, takes a large graph and a small graph , and produces a graph that approximately inherits the size of the large one but the degree of the small one...
and prove its properties.
Given a vertex
 and an edge label
and an edge label  , the rotation map returns the
, the rotation map returns the  'th neighbor of
'th neighbor of  and the edge label that would lead back to
and the edge label that would lead back to  .
.Definition
For a D-regular graph G, the rotation map is defined as follows:
is defined as follows: 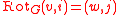 if the ith edge leaving v leads to w, and the jth edge leaving w leads to v.
if the ith edge leaving v leads to w, and the jth edge leaving w leads to v.Basic properties
From the definition we see that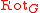 is a permutation, and moreover
is a permutation, and moreover 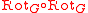 is the identity map.
is the identity map.Special cases and properties
- A rotation map is consistently labeled if all of the edges leaving each vertex are labeled in such a way that at each vertex, the labels of the incoming edges are all distinct. Every regular graph has some consistent labeling.
- A rotation map is
 -consistent if
-consistent if  . From the definition, a
. From the definition, a  -consistent rotation map is consistently labeled.
-consistent rotation map is consistently labeled.

