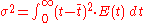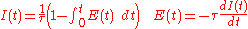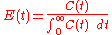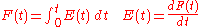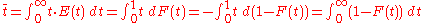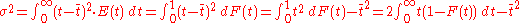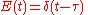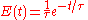
Residence Time Distribution
Encyclopedia
The residence time distribution (RTD) of a chemical reactor
is a probability distribution function that describes the amount of time a fluid
element could spend inside the reactor. Chemical engineers
use the RTD to characterize the mixing and flow within reactors and to compare the behavior of real reactors to their ideal models. This is useful, not only for troubleshooting existing reactors, but in estimating the yield of a given reaction and designing future reactors.
The concept was first proposed by MacMullin and Weber in 1935, but was not used extensively until P.V. Danckwerts
analyzed a number of important RTDs in 1953.
The theory of residence time distributions generally begins with three assumptions:
The incompressibility assumption is not required, but compressible flows are more difficult to work with and less common in chemical processes. A further level of complexity is required for multi-phase reactors, where a separate RTD will describe the flow of each phase, for example bubbling air through a liquid.
The distribution of residence time
s is represented by an exit age distribution,
. The function 
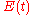has the units of time-1 and is defined such that
The fraction of the fluid that spends a given duration,
inside the reactor is given by the value of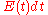 
.
The fraction of the fluid that leaves the reactor with an age less than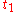
is
The fraction of the fluid that leaves the reactor with an age greater than
is
The average residence time is given by the first moment
of the age distribution:
If there are no dead, or stagnant, zones within the reactor then
will be equal to 
, the residence time
calculated from the total reactor volume and the volumetric flow rate of the fluid:
The higher order central moment
s can provide significant information about the behavior of the function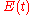
. For example, the second central moment indicates the variance (
), the degree of dispersion around the mean.
The third central moment indicates the skewness
of the RTD and the fourth central moment indicates the kurtosis
(the "peakedness").
One can also define an internal age distribution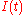
that describes the reactor contents. This function has a similar definition as 
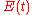: the fraction of fluid within the reactor with an age of 
is 
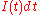. As shown by Danckwerts, the relation between 
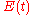and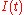 
can be found from the mass balance:
In general, the change in tracer concentration will either be a pulse or a step. Other functions are possible, but they require more calculations to deconvolute
the RTD curve,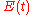
.
. Although an infinitely short injection cannot be produced, it can be made much smaller than the mean residence time of the vessel. If a mass of tracer,
, is introduced into a vessel of volume 
and an expected residence
time of
, the resulting curve of 
can be transformed into a dimensionless residence time distribution curve by the following relation:
. The concentration of tracer at the outlet is measured and normalized to the concentration 
to obtain the non-dimensional curve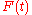 
which goes from 0 to 1:
The step- and pulse-responses of a reactor are related by the following:
The value of the mean residence time and the variance can also be deduced from the function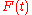
:
A step experiment is often easier to perform than a pulse experiment, but it tends to smooth over some of the details that a pulse response could show. It is easy to numerically integrate an experimental pulse response to obtain a very high-quality estimate of the step response, but the reverse is not the case because any noise in the concentration measurement will be amplified by numeric differentiation.
and the continuous stirred-tank reactor (CSTR), or mixed-flow reactor. This characteristic is important in order to calculate the performance of a reaction with known kinetics.
there is no axial mixing and the fluid elements leave in the same order they arrived. Therefore, fluid entering the reactor at time
will exit the reactor at time 
, where 
is the residence time of the reactor. The residence time distribution function is therefore a dirac delta function
at
.
The variance of an ideal plug-flow reactor is zero.
The RTD of a real reactor deviate from that of an ideal reactor, depending on the hydrodynamics within the vessel. A non-zero variance indicates that there is some dispersion along the path of the fluid, which may be attributed to turbulence, a non-uniform velocity profile, or diffusion. If the mean of the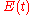
curve arrives earlier than the expected time 
it indicates that there is stagnant fluid within the vessel. If the RTD curve shows more than one main peak it may indicate channeling, parallel paths to the exit, or strong internal circulation.
In reality, it is impossible to obtain such rapid mixing, especially on industrial scales where reactor vessels may range between 1 and several tens of cubic meters, and hence the RTD of a real reactor will deviate from the ideal exponential decay. For example, there will be some finite delay before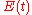
reaches its maximum value and the length of the delay will reflect the rate of mass transfer within the reactor. Just as was noted for a plug-flow reactor, an early mean will indicate some stagnant fluid within the vessel, while the presence of multiple peaks could indicate channeling, parallel paths to the exit, or strong internal circulation. Short-circuiting fluid within the reactor would appear in an RTD curve as a small pulse of concentrated tracer that reaches the outlet shortly after injection.
t = (Mean Concentration in Ocean) × (Ocean Volume) / (Input per year)
where the ocean volume is (1.37×10^21 L).
The input sums all inputs to the ocean. For many elements, the major input is from rivers and the input per year is the Mean River Concentration × Continental Runoff Rate. If the concentration of an element is not changing, then the Input and Output of an element must be equal (steady state). The residence time can then be calculated using the estimated output, if that is known.
Chemical reactor
In chemical engineering, chemical reactors are vessels designed to contain chemical reactions. The design of a chemical reactor deals with multiple aspects of chemical engineering. Chemical engineers design reactors to maximize net present value for the given reaction...
is a probability distribution function that describes the amount of time a fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
element could spend inside the reactor. Chemical engineers
Chemical engineering
Chemical engineering is the branch of engineering that deals with physical science , and life sciences with mathematics and economics, to the process of converting raw materials or chemicals into more useful or valuable forms...
use the RTD to characterize the mixing and flow within reactors and to compare the behavior of real reactors to their ideal models. This is useful, not only for troubleshooting existing reactors, but in estimating the yield of a given reaction and designing future reactors.
The concept was first proposed by MacMullin and Weber in 1935, but was not used extensively until P.V. Danckwerts
Peter Victor Danckwerts
Peter Victor Danckwerts GC, MBE, FRS was Shell Professor of Chemical Engineering at Cambridge University from 1959 to 1977 and a Fellow of Pembroke College, Cambridge....
analyzed a number of important RTDs in 1953.
Theory
- the reactor is at steady-state,
- transports at the inlet and the outlet takes place only by advectionAdvectionAdvection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries...
, and - the fluid is incompressible.
The incompressibility assumption is not required, but compressible flows are more difficult to work with and less common in chemical processes. A further level of complexity is required for multi-phase reactors, where a separate RTD will describe the flow of each phase, for example bubbling air through a liquid.
The distribution of residence time
Residence time
Residence time is the average amount of time that a particle spends in a particular system. This measurement varies directly with the amount of substance that is present in the system....
s is represented by an exit age distribution,
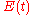. The function has the units of time-1 and is defined such that
-
.
The fraction of the fluid that spends a given duration,
inside the reactor is given by the value of 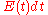.The fraction of the fluid that leaves the reactor with an age less than
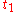is
-
.
The fraction of the fluid that leaves the reactor with an age greater than
is
-
.
The average residence time is given by the first moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the age distribution:
-
.
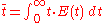If there are no dead, or stagnant, zones within the reactor then
will be equal to , the residence timeResidence time
Residence time is the average amount of time that a particle spends in a particular system. This measurement varies directly with the amount of substance that is present in the system....
calculated from the total reactor volume and the volumetric flow rate of the fluid:
-
.
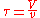The higher order central moment
Central moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
s can provide significant information about the behavior of the function
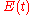. For example, the second central moment indicates the variance (), the degree of dispersion around the mean.
The third central moment indicates the skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
of the RTD and the fourth central moment indicates the kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
(the "peakedness").
One can also define an internal age distribution
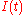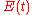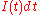that describes the reactor contents. This function has a similar definition as : the fraction of fluid within the reactor with an age of is . As shown by Danckwerts, the relation between 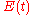and 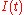can be found from the mass balance:
Determining the RTD Experimentally
Residence time distributions are measured by introducing a non-reactive tracer into the system at the inlet. The concentration of the tracer is changed according to a known function and the response is found by measuring the concentration of the tracer at the outlet. The selected tracer should not modify the physical characteristics of the fluid (equal density, equal viscosity) and the introduction of the tracer should not modify the hydrodynamic conditions.In general, the change in tracer concentration will either be a pulse or a step. Other functions are possible, but they require more calculations to deconvolute
Deconvolution
In mathematics, deconvolution is an algorithm-based process used to reverse the effects of convolution on recorded data. The concept of deconvolution is widely used in the techniques of signal processing and image processing...
the RTD curve,
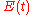.Pulse Experiments
This method required the introduction of a very small volume of concentrated tracer at the inlet of the reactor, such that it approaches the dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. Although an infinitely short injection cannot be produced, it can be made much smaller than the mean residence time of the vessel. If a mass of tracer,
, is introduced into a vessel of volume and an expected residencetime of
, the resulting curve of can be transformed into a dimensionless residence time distribution curve by the following relation:
Step Experiments
In a step experiment the concentration of tracer at the reactor inlet changes abruptly from 0 to. The concentration of tracer at the outlet is measured and normalized to the concentration to obtain the non-dimensional curve 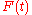which goes from 0 to 1:
-
.
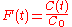The step- and pulse-responses of a reactor are related by the following:
The value of the mean residence time and the variance can also be deduced from the function
:
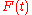A step experiment is often easier to perform than a pulse experiment, but it tends to smooth over some of the details that a pulse response could show. It is easy to numerically integrate an experimental pulse response to obtain a very high-quality estimate of the step response, but the reverse is not the case because any noise in the concentration measurement will be amplified by numeric differentiation.
RTDs of ideal and real reactors
The residence time distribution of a reactor can be used to compare its behavior to that of two ideal reactor models: the plug-flow reactorPlug flow reactor model
The plug flow reactor model is used to describe chemical reactions in continuous, flowing systems. The PFR model is used to predict the behaviour of chemical reactors, so that key reactor variables, such as the dimensions of the reactor, can be estimated...
and the continuous stirred-tank reactor (CSTR), or mixed-flow reactor. This characteristic is important in order to calculate the performance of a reaction with known kinetics.
Plug Flow Reactors
In an ideal plug-flow reactorPlug flow reactor model
The plug flow reactor model is used to describe chemical reactions in continuous, flowing systems. The PFR model is used to predict the behaviour of chemical reactors, so that key reactor variables, such as the dimensions of the reactor, can be estimated...
there is no axial mixing and the fluid elements leave in the same order they arrived. Therefore, fluid entering the reactor at time
will exit the reactor at time , where is the residence time of the reactor. The residence time distribution function is therefore a dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
at
.
The variance of an ideal plug-flow reactor is zero.
The RTD of a real reactor deviate from that of an ideal reactor, depending on the hydrodynamics within the vessel. A non-zero variance indicates that there is some dispersion along the path of the fluid, which may be attributed to turbulence, a non-uniform velocity profile, or diffusion. If the mean of the
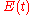curve arrives earlier than the expected time it indicates that there is stagnant fluid within the vessel. If the RTD curve shows more than one main peak it may indicate channeling, parallel paths to the exit, or strong internal circulation.Mixed Flow Reactors
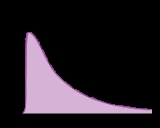
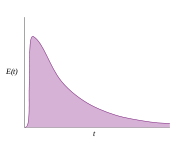
An ideal continuous stirred-tank reactor is based on the assumption that the flow at the inlet is completely and instantly mixed into the bulk of the reactor. The reactor and the outlet fluid have identical, homogeneous compositions at all times. An ideal CSTR has an exponential residence time distribution:
In reality, it is impossible to obtain such rapid mixing, especially on industrial scales where reactor vessels may range between 1 and several tens of cubic meters, and hence the RTD of a real reactor will deviate from the ideal exponential decay. For example, there will be some finite delay before
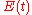reaches its maximum value and the length of the delay will reflect the rate of mass transfer within the reactor. Just as was noted for a plug-flow reactor, an early mean will indicate some stagnant fluid within the vessel, while the presence of multiple peaks could indicate channeling, parallel paths to the exit, or strong internal circulation. Short-circuiting fluid within the reactor would appear in an RTD curve as a small pulse of concentrated tracer that reaches the outlet shortly after injection.Oceanographic
In chemical oceanography, residence time (t) of an element is defined as the amount of an element in the ocean at steady state divided by the rate at which that element is added to the ocean:t = (Mean Concentration in Ocean) × (Ocean Volume) / (Input per year)
where the ocean volume is (1.37×10^21 L).
The input sums all inputs to the ocean. For many elements, the major input is from rivers and the input per year is the Mean River Concentration × Continental Runoff Rate. If the concentration of an element is not changing, then the Input and Output of an element must be equal (steady state). The residence time can then be calculated using the estimated output, if that is known.