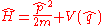Relation between Schrödinger's equation and the path integral formulation of quantum mechanics
Encyclopedia
This article relates the Schrödinger equation
with the path integral formulation of quantum mechanics using a simple nonrelativistic one-dimensional single-particle Hamiltonian
composed of kinetic and potential energy.
, is

where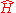 is the Hamiltonian operator. We have assumed for simplicity that there is only one spatial dimension.
is the Hamiltonian operator. We have assumed for simplicity that there is only one spatial dimension.
The Hamiltonian operator can be written
where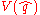 is the potential energy
is the potential energy
, m is the mass and we have assumed for simplicity that there is only one spatial dimension q.
The formal solution of the equation is

where we have assumed the initial state is a free-particle spatial state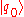 .
.
The transition probability amplitude
for a transition from an initial state to a final free-particle spatial state
to a final free-particle spatial state 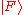 at time T is
at time T is
 .
.
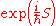
over all possible paths from the initial state to the final state. Here S is the classical action
.
The reformulation of this transition amplitude, originally due to Dirac and conceptualized by Feynman, forms the basis of the path integral formulation.
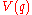 , commutes
, commutes
with the momentum,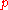 ). Following Feynman, this derivation can be made rigorous by writing the momentum,
). Following Feynman, this derivation can be made rigorous by writing the momentum, 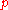 , as the product of mass,
, as the product of mass,  , and a difference in position at two points,
, and a difference in position at two points, 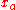 and
and 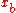 , separated by a time difference,
, separated by a time difference,  , thus quantizing distance
, thus quantizing distance
.
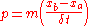
Note 2: There are two errata on page 11 in Zee, both of which are corrected here.
We can divide the time interval from 0 to T into N segments of length
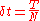 .
.
The transition amplitude can then be written
 .
.
We can insert the identity
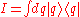
matrix N-1 times between the exponentials to yield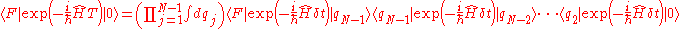 .
.
Each individual transition probability can be written
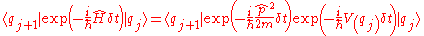 .
.
We can insert the identity
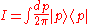
into the amplitude to yield
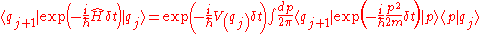
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
with the path integral formulation of quantum mechanics using a simple nonrelativistic one-dimensional single-particle Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
composed of kinetic and potential energy.
Schrödinger's equation
Schrödinger's equation, in bra-ket notationBra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
, is

where
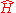 is the Hamiltonian operator. We have assumed for simplicity that there is only one spatial dimension.
is the Hamiltonian operator. We have assumed for simplicity that there is only one spatial dimension.The Hamiltonian operator can be written
where
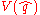 is the potential energy
is the potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, m is the mass and we have assumed for simplicity that there is only one spatial dimension q.
The formal solution of the equation is

where we have assumed the initial state is a free-particle spatial state
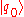 .
.The transition probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
for a transition from an initial state
 to a final free-particle spatial state
to a final free-particle spatial state 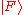 at time T is
at time T is .
.Path integral formulation
The path integral formulation states that the transition amplitude is simply the integral of the quantity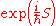
over all possible paths from the initial state to the final state. Here S is the classical action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
.
The reformulation of this transition amplitude, originally due to Dirac and conceptualized by Feynman, forms the basis of the path integral formulation.
From Schrödinger's equation to the path integral formulation
Note: the following derivation is heuristic (it is valid in cases in which the potential,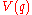 , commutes
, commutesCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
with the momentum,
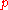 ). Following Feynman, this derivation can be made rigorous by writing the momentum,
). Following Feynman, this derivation can be made rigorous by writing the momentum, 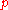 , as the product of mass,
, as the product of mass,  , and a difference in position at two points,
, and a difference in position at two points, 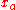 and
and 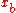 , separated by a time difference,
, separated by a time difference,  , thus quantizing distance
, thus quantizing distanceSpatial quantization
In quantum mechanics, spatial quantization is the quantization of angular momentum in three-dimensional space. It results from the fact that the angular momentum of a rigid rotor is expressed in three dimensions, and is quantized....
.
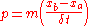
Note 2: There are two errata on page 11 in Zee, both of which are corrected here.
We can divide the time interval from 0 to T into N segments of length
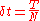 .
.The transition amplitude can then be written
 .
.We can insert the identity
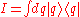
matrix N-1 times between the exponentials to yield
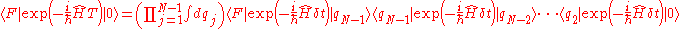 .
.Each individual transition probability can be written
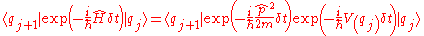 .
.We can insert the identity
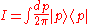
into the amplitude to yield
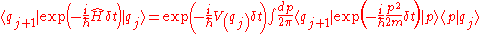
-
-
-
-
-
-
-
-
-

-
-
-
-
-
-
-
-
-

where we have used the fact that the free particle wave function is
-
 .
.
The integral over p can be performed (see Common integrals in quantum field theoryCommon integrals in quantum field theoryThere are common integrals in quantum field theory that appear repeatedly. These integrals are all variations and generalizations of gaussian integrals to the complex plane and to multiple dimensions. Other integrals can be approximated by versions of the gaussian integral...
) to obtain
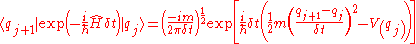
The transition amplitude for the entire time period is
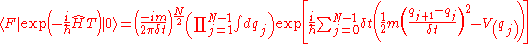 .
.
If we take the limit of large N the transition amplitude reduces to

where S is the classical actionAction (physics)In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
given by
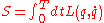
and L is the classical LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
given by
 .
.
The integral
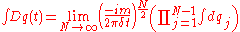
is an integral over all possible paths the particle may take in going from its initial state to its final state. This expression actually defines the manner in which the path integrals are to be taken. The coefficient of the integral is a normalization factor and has no significance.
This recovers the path integral formulation from Schrödinger's equation.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-