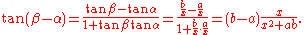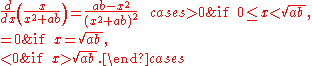Regiomontanus' angle maximization problem
Encyclopedia
In mathematics
, the Regiomontanus' angle maximization problem, is a famous optimization
problem posed by the 15th-century German mathematician Johannes Müller (also known as Regiomontanus
). The problem is as follows:
If the viewer stands too close to the wall or too far from the wall, the angle is small; somewhere in between it is as large as possible.
The same approach applies to finding the optimal place from which to kick a ball in rugby. For that matter, it is not necessary that the alignment
of the picture be at right angles: we might be looking at a window of the Leaning Tower of Pisa or a realtor showing off the
advantages of a sky-light in a sloping attic roof.
passing through the top and bottom of the painting and tangent to the eye-level line. By elementary geometry, if the viewer's position were to move along the circle, the angle subtended by the painting would remain constant
. All positions on the eye-level line except the point of tangency are outside of the circle, and therefore the angle subtended by the painting from those points is smaller.
By Elements
III.36 (alternatively the power-of-a-point theorem
), the distance from the wall to the point of tangency is the geometric mean
of the heights of the top and bottom of the painting. This means, in turn, that if we reflect the bottom of the picture in the line at eye-level and draw the circle with the segment between the top of the picture and this reflected point as diameter, the circle intersects the line at eye-level in the required position (by Elements II.14).
Let
The angle we seek to maximize is β − α. The tangent of the angle increases as the angle increases; therefore it suffices to maximize
Since b − a is a positive constant, we only need to maximize the fraction that follows it. Differentiating, we get
Therefore the angle increases as x goes from 0 to √(ab) and decreases as x increases from √(ab). The angle is therefore as large as possible precisely when x = √(ab), the geometric mean
of a and b.
This is equivalent to minimizing the reciprocal:
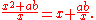
Observe that this last quantity is equal to
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Regiomontanus' angle maximization problem, is a famous optimization
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
problem posed by the 15th-century German mathematician Johannes Müller (also known as Regiomontanus
Regiomontanus
Johannes Müller von Königsberg , today best known by his Latin toponym Regiomontanus, was a German mathematician, astronomer, astrologer, translator and instrument maker....
). The problem is as follows:
- A painting hangs from a wall. Given the heights of the top and bottom of the painting above the viewer's eye level, how far from the wall should the viewer stand in order to maximize the angle subtended by the painting and whose vertex is at the viewer's eye?
If the viewer stands too close to the wall or too far from the wall, the angle is small; somewhere in between it is as large as possible.
The same approach applies to finding the optimal place from which to kick a ball in rugby. For that matter, it is not necessary that the alignment
of the picture be at right angles: we might be looking at a window of the Leaning Tower of Pisa or a realtor showing off the
advantages of a sky-light in a sloping attic roof.
Solution by elementary geometry
There is a unique circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
passing through the top and bottom of the painting and tangent to the eye-level line. By elementary geometry, if the viewer's position were to move along the circle, the angle subtended by the painting would remain constant
Inscribed angle
In geometry, an inscribed angle is formed when two secant lines of a circle intersect on the circle....
. All positions on the eye-level line except the point of tangency are outside of the circle, and therefore the angle subtended by the painting from those points is smaller.
By Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
III.36 (alternatively the power-of-a-point theorem
Power of a point
In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...
), the distance from the wall to the point of tangency is the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of the heights of the top and bottom of the painting. This means, in turn, that if we reflect the bottom of the picture in the line at eye-level and draw the circle with the segment between the top of the picture and this reflected point as diameter, the circle intersects the line at eye-level in the required position (by Elements II.14).
Solution by calculus
In the present day, this problem is widely known because it appears as an exercise in many first-year calculus textbooks (for example that of Stewart ).Let
- a = the height of the bottom of the painting above eye level;
- b = the height of the top of the painting above eye level;
- x = the viewer's distance from the wall;
- α = the angle of elevation of the bottom of the painting, seen from the viewer's position;
- β = the angle of elevation of the top of the painting, seen from the viewer's position.
The angle we seek to maximize is β − α. The tangent of the angle increases as the angle increases; therefore it suffices to maximize
Since b − a is a positive constant, we only need to maximize the fraction that follows it. Differentiating, we get
Therefore the angle increases as x goes from 0 to √(ab) and decreases as x increases from √(ab). The angle is therefore as large as possible precisely when x = √(ab), the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of a and b.
Solution by algebra
We have seen that it suffices to maximizeThis is equivalent to minimizing the reciprocal:
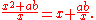
Observe that this last quantity is equal to
-
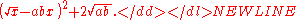
This is as small as possible precisely when the square is 0, and that happens when x = √(ab).
Alternatively, we might cite this as an instance of the inequality between the arithmetic and geometric means.