Reduction of order
Encyclopedia
Reduction of order is a technique in mathematics
for solving second-order linear ordinary
differential equations
. It is employed when one solution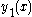
is known and a second linearly independent
solution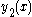
is desired.
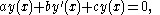
where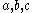
are real non-zero coefficients. Furthermore, assume that the associated characteristic equation
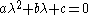
has repeated roots (i.e. the discriminant
,
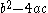, vanishes). Thus we have
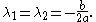
Thus our one solution to the ODE is
To find a second solution we take as a guess
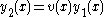
where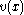
is an unknown function to be determined. Since 
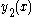must satisfy the original ODE, we substitute it back in to get
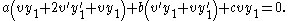
Rearranging this equation in terms of the derivatives of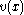
we get
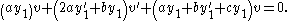
Since we know that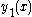
is a solution to the original problem, the coefficient of the last term is equal to zero. Furthermore, substituting 
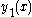into the second term's coefficient yields (for that coefficient)
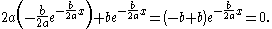
Therefore we are left with
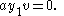
Since
is assumed non-zero and 
is an exponential function
and thus never equal to zero we simply have
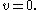
This can be integrated twice to yield
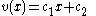
where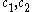
are constants of integration. We now can write our second solution as
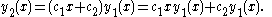
Since the second term in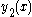
is a scalar multiple of the first solution (and thus linearly dependent) we can drop that term, yielding a final solution of
Finally, we can prove that the second solution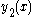
found via this method is linearly independent of the first solution by calculating the Wronskian
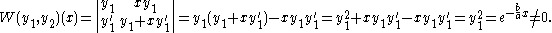
Thus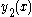
is the second linearly independent solution we were looking for.
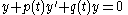
and a single solution (
), let the second solution be defined
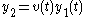
where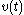
is an arbitrary function. Thus
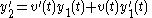
and
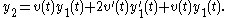
If these are substituted for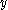
, 
, and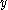 
in the differential equation, then
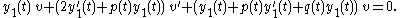
Since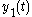
is a solution of the original differential equation, 
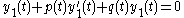, so we can reduce to
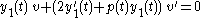
which is a first-order differential equation for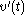
(reduction of order). Divide by 
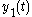, obtaining
.
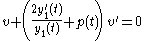Integrating factor :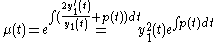
.
Multiplying the differential equation with the integrating factor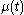
, the equation in 
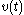can be reduced to
.
Once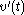
is solved, integrate it and enter into the original equation for 
:
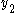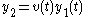where 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
for solving second-order linear ordinary
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
differential equations
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
. It is employed when one solution
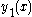is known and a second linearly independentLinear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
solution
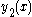is desired.An Example
Consider the general second-order linear constant coefficient ODE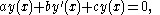where
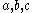are real non-zero coefficients. Furthermore, assume that the associated characteristic equation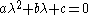has repeated roots (i.e. the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
,
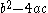, vanishes). Thus we have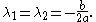Thus our one solution to the ODE is
To find a second solution we take as a guess
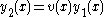
where
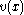is an unknown function to be determined. Since 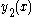must satisfy the original ODE, we substitute it back in to get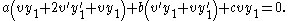Rearranging this equation in terms of the derivatives of
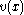we get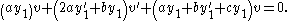Since we know that
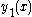is a solution to the original problem, the coefficient of the last term is equal to zero. Furthermore, substituting 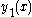into the second term's coefficient yields (for that coefficient)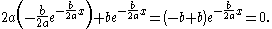Therefore we are left with
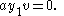
Since
is assumed non-zero and is an exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and thus never equal to zero we simply have
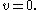
This can be integrated twice to yield
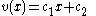
where
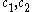are constants of integration. We now can write our second solution as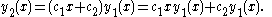Since the second term in
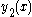is a scalar multiple of the first solution (and thus linearly dependent) we can drop that term, yielding a final solution ofFinally, we can prove that the second solution
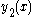found via this method is linearly independent of the first solution by calculating the WronskianWronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
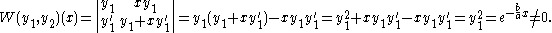
Thus
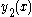is the second linearly independent solution we were looking for.General method
Given a linear differential equation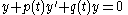and a single solution (
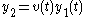
), let the second solution be definedwhere
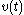is an arbitrary function. Thus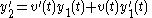and
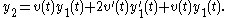
If these are substituted for
, , and 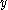in the differential equation, then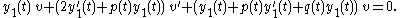Since
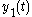is a solution of the original differential equation, 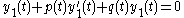, so we can reduce to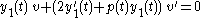which is a first-order differential equation for
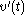(reduction of order). Divide by 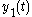, obtaining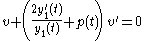.Integrating factor :
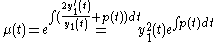.Multiplying the differential equation with the integrating factor
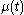, the equation in 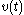can be reduced to.Once
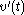is solved, integrate it and enter into the original equation for 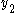: 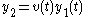where .