
Reduction criterion
Encyclopedia
In quantum information theory, the reduction criterion is a necessary condition a mixed state must satisfy in order for it to be separable. In other words, the reduction criterion is a separability criterion.
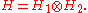
An (un-normalized) mixed state ρ is a positive linear operator (density matrix) acting on H.
A linear map Φ: L(H2) → L(H1) is said to be positive if it preserves the cone of positive elements, i.e. A is positive implied Φ(A) is also.
From the one-to-one correspondence between positive maps and entanglement witness
es, we have that a state ρ is entangled if and only if there exists a positive map Φ such that
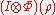
is not positive. Therefore, if ρ is separable, then for all positive map Φ,
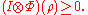
Thus every positive, but not completely positive, map Φ gives rise to a necessariy condition for separability in this way. The reduction criterion is a particular example of this.
Suppose H1 = H2. Define the positive map Φ: L(H2) → L(H1) by

It is known that Φ is positive but not completely positive. So a mixed state ρ being separable implies
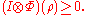
Direct calculation shows that the above expression is same as
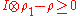
where ρ1 is the partial trace
of ρ with respect to the second system. The dual relation

is obtained in the analogous fashion. The reduction criterion consists of the above two inequalities.
Details
Let H1 and H2 be Hilbert spaces of finite dimensions n and m respectively. L(Hi) will denote the space of linear operators acting on Hi. Consider a bipartite quantum syste whose state space is the tensor product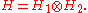
An (un-normalized) mixed state ρ is a positive linear operator (density matrix) acting on H.
A linear map Φ: L(H2) → L(H1) is said to be positive if it preserves the cone of positive elements, i.e. A is positive implied Φ(A) is also.
From the one-to-one correspondence between positive maps and entanglement witness
Entanglement witness
In quantum information theory, an entanglement witness is an object of geometric nature which distinguishes an entangled state from separable ones.- Details :...
es, we have that a state ρ is entangled if and only if there exists a positive map Φ such that
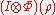
is not positive. Therefore, if ρ is separable, then for all positive map Φ,
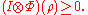
Thus every positive, but not completely positive, map Φ gives rise to a necessariy condition for separability in this way. The reduction criterion is a particular example of this.
Suppose H1 = H2. Define the positive map Φ: L(H2) → L(H1) by

It is known that Φ is positive but not completely positive. So a mixed state ρ being separable implies
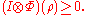
Direct calculation shows that the above expression is same as
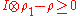
where ρ1 is the partial trace
Partial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
of ρ with respect to the second system. The dual relation

is obtained in the analogous fashion. The reduction criterion consists of the above two inequalities.

