
Reduced cost
Encyclopedia
In linear programming
, reduced cost, or opportunity cost, is the amount by which an objective function coefficient would have to improve (so increase for maximization problem, decrease for minimization problem) before it would be possible for a corresponding variable to assume a positive value in the optimal solution. It is the cost for increasing a variable by a small amount, i.e., the first derivative from a certain point on the polyhedron
that constrains the problem. When the point is a vertex in the polyhedron, the variable with the most extreme cost, negatively for minimisation and positively maximisation, is sometimes referred to as the steepest edge.
Given a system minimize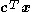 subject to
subject to  , the reduced cost vector can be computed as
, the reduced cost vector can be computed as 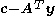 , where
, where 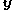 is the dual cost vector.
is the dual cost vector.
It follows directly that for a minimisation problem, any non-basic variables at their lower bounds with strictly negative reduced costs are eligible to enter that basis, while any basic variables must have a reduced cost that is exactly 0. For a maximisation problem, the non-basic variables at their lower bounds that are eligible for entering the basis have a strictly positive reduced cost.
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
, reduced cost, or opportunity cost, is the amount by which an objective function coefficient would have to improve (so increase for maximization problem, decrease for minimization problem) before it would be possible for a corresponding variable to assume a positive value in the optimal solution. It is the cost for increasing a variable by a small amount, i.e., the first derivative from a certain point on the polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
that constrains the problem. When the point is a vertex in the polyhedron, the variable with the most extreme cost, negatively for minimisation and positively maximisation, is sometimes referred to as the steepest edge.
Given a system minimize
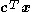 subject to
subject to  , the reduced cost vector can be computed as
, the reduced cost vector can be computed as 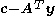 , where
, where 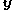 is the dual cost vector.
is the dual cost vector.It follows directly that for a minimisation problem, any non-basic variables at their lower bounds with strictly negative reduced costs are eligible to enter that basis, while any basic variables must have a reduced cost that is exactly 0. For a maximisation problem, the non-basic variables at their lower bounds that are eligible for entering the basis have a strictly positive reduced cost.

