
Rayleigh flow
Encyclopedia
Rayleigh flow refers to diabatic
flow through a constant area duct where the effect of heat addition or rejection is considered. Compressibility
effects often come into consideration, although the Rayleigh flow model certainly also applies to incompressible flow
. For this model, the duct area remains constant and no mass is added within the duct. Therefore, unlike Fanno flow
, the stagnation temperature
is a variable. The heat addition causes a decrease in stagnation pressure
, which is known as the Rayleigh effect and is critical in the design of combustion systems. Heat addition will cause both supersonic
and subsonic
Mach number
s to approach Mach 1, resulting in choked flow
. Conversely, heat rejection decreases a subsonic Mach number and increases a supersonic Mach number along the duct. It can be shown that for calorically perfect flows the maximum entropy
occurs at M
= 1. Rayleigh flow is named after John Strutt, 3rd Baron Rayleigh
.
 The Rayleigh flow model begins with a differential equation
The Rayleigh flow model begins with a differential equation
that relates the change in Mach number with the change in stagnation temperature
, T0. The differential equation is shown below.
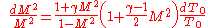
Solving the differential equation leads to the relation shown below, where T0* is the stagnation temperature at the throat location of the duct which is required for thermally choking the flow.
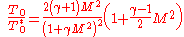
These values are significant in the design of combustion systems. For example, if a turbojet combustion chamber has a maximum temperature of T0* = 2000 K, T0 and M at the entrance to the combustion chamber must be selected so thermal choking does not occur, which will limit the mass flow rate of air into the engine and decrease thrust.
For the Rayleigh flow model, the dimensionless change in entropy relation is shown below.
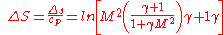
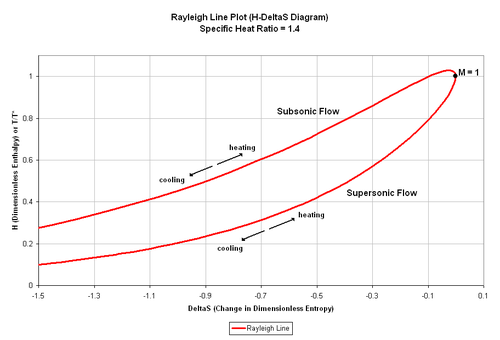
The above equation can be used to plot the Rayleigh line on a Mach number versus ΔS graph, but the dimensionless enthalpy, H, versus ΔS diagram is more often used. The dimensionless enthalpy equation is shown below with an equation relating the static temperature with its value at the choke location for a calorically perfect gas where the heat capacity at constant pressure, cp, remains constant.
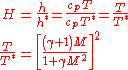
The above equation can be manipulated to solve for M as a function of H. However, due to the form of the T/T* equation, a complicated multi-root relation is formed for M = M(T/T*). Instead, M can be chosen as an independent variable where ΔS and H can be matched up in a chart as shown in Figure 1. Figure 1 shows that heating will increase an upstream, subsonic
Mach number until M = 1.0 and the flow chokes
. Conversely, adding heat to a duct with an upstream, supersonic
Mach number will cause the Mach number to decrease until the flow chokes. Cooling produces the opposite result for each of those two cases. The Rayleigh flow model reaches maximum entropy at M = 1.0 For subsonic flow, the maximum value of H occurs at M = 0.845. This indicates that cooling, instead of heating, causes the Mach number to move from 0.845 to 1.0 This is not necessarily correct as the stagnation temperature always increases to move the flow from a subsonic Mach number to M = 1, but from M = 0.845 to M = 1.0 the flow accelerates faster than heat is added to it. Therefore, this is a situation where heat is added but T/T* decreases in that region.
 The area and mass flow rate are held constant for Rayleigh flow. Unlike Fanno flow, the Fanning friction factor, f, remains constant. These relations are shown below with the * symbol representing the throat location where choking can occur.
The area and mass flow rate are held constant for Rayleigh flow. Unlike Fanno flow, the Fanning friction factor, f, remains constant. These relations are shown below with the * symbol representing the throat location where choking can occur.
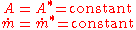
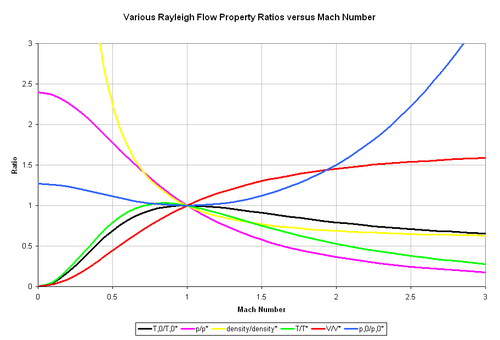
Differential equations can also be developed and solved to describe Rayleigh flow property ratios with respect to the values at the choking location. The ratios for the pressure, density, static temperature, velocity and stagnation pressure are shown below, respectively. They are represented graphically along with the stagnation temperature ratio equation from the previous section. A stagnation property contains a '0' subscript.
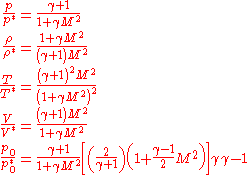
 The Rayleigh flow model has many analytical uses, most notably involving aircraft engines. For instance, the combustion chambers inside turbojet engines usually have a constant area and the fuel mass addition is negligible. These properties make the Rayleigh flow model applicable for heat addition to the flow through combustion, assuming the heat addition does not result in dissociation
The Rayleigh flow model has many analytical uses, most notably involving aircraft engines. For instance, the combustion chambers inside turbojet engines usually have a constant area and the fuel mass addition is negligible. These properties make the Rayleigh flow model applicable for heat addition to the flow through combustion, assuming the heat addition does not result in dissociation
of the air-fuel mixture. Producing a shock wave inside the combustion chamber of an engine due to thermal choking is very undesirable due to the decrease in mass flow rate and thrust. Therefore, the Rayleigh flow model is critical for an initial design of the duct geometry and combustion temperature for an engine.
The Rayleigh flow model is also used extensively with the Fanno flow
model. These two models intersect at points on the enthalpy-entropy and Mach number-entropy diagrams, which is meaningful for many applications. However, the entropy values for each model are not equal at the sonic state. The change in entropy is 0 at M = 1 for each model, but the previous statement means the change in entropy from the same arbitrary point to the sonic point is different for the Fanno and Rayleigh flow models. If initial values of si and Mi are defined, a new equation for dimensionless entropy versus Mach number can be defined for each model. These equations are shown below for Fanno and Rayleigh flow, respectively.
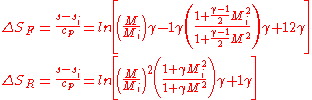
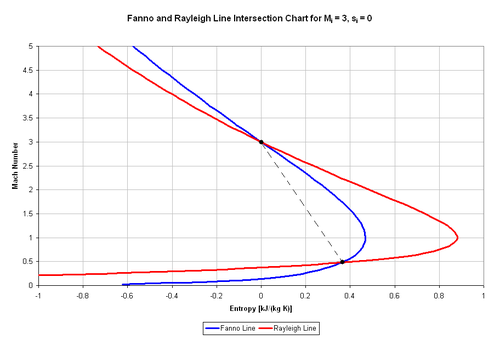
Figure 3 shows the Rayleigh and Fanno lines intersecting with each other for initial conditions of si = 0 and Mi = 3.0 The intersection points are calculated by equating the new dimensionless entropy equations with each other, resulting in the relation below.
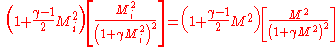
Interestingly, the intersection points occur at the given initial Mach number and its post-normal shock value. For Figure 3, these values are M = 3.0 and 0.4752, which can be found the normal shock tables listed in most compressible flow textbooks. A given flow with a constant duct area can switch between the Rayleigh and Fanno models at these points.
Diabatic
A diabatic process is one in which heat transfer takes place, which is the opposite of an adiabatic process. In quantum chemistry, the potential energy surfaces are obtained within the adiabatic or Born-Oppenheimer approximation...
flow through a constant area duct where the effect of heat addition or rejection is considered. Compressibility
Compressible flow
Compressible flow is the area of fluid mechanics that deals with fluids in which the fluid density varies significantly in response to a change in pressure. Compressibility effects are typically considered significant if the Mach number of the flow exceeds 0.3, or if the fluid undergoes very large...
effects often come into consideration, although the Rayleigh flow model certainly also applies to incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
. For this model, the duct area remains constant and no mass is added within the duct. Therefore, unlike Fanno flow
Fanno flow
Fanno flow refers to adiabatic flow through a constant area duct where the effect of friction is considered. Compressibility effects often come into consideration, although the Fanno flow model certainly also applies to incompressible flow. For this model, the duct area remains constant, the flow...
, the stagnation temperature
Stagnation temperature
In thermodynamics and fluid mechanics, stagnation temperature is the temperature at a stagnation point in a fluid flow. At a stagnation point the speed of the fluid is zero and all of the kinetic energy has been converted to internal energy and is added to the local static enthalpy...
is a variable. The heat addition causes a decrease in stagnation pressure
Stagnation pressure
In fluid dynamics, stagnation pressure is the static pressure at a stagnation point in a fluid flow.At a stagnation point the fluid velocity is zero and all kinetic energy has been converted into pressure energy . Stagnation pressure is equal to the sum of the free-stream dynamic pressure and...
, which is known as the Rayleigh effect and is critical in the design of combustion systems. Heat addition will cause both supersonic
Supersonic
Supersonic speed is a rate of travel of an object that exceeds the speed of sound . For objects traveling in dry air of a temperature of 20 °C this speed is approximately 343 m/s, 1,125 ft/s, 768 mph or 1,235 km/h. Speeds greater than five times the speed of sound are often...
and subsonic
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
Mach number
Mach number
Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
s to approach Mach 1, resulting in choked flow
Choked flow
Choked flow is a compressible flow effect. The parameter that becomes "choked" or "limited" is the velocity or the mass flow rate.Choked flow is a fluid dynamic condition associated with the Venturi effect...
. Conversely, heat rejection decreases a subsonic Mach number and increases a supersonic Mach number along the duct. It can be shown that for calorically perfect flows the maximum entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
occurs at M
Mach number
Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
= 1. Rayleigh flow is named after John Strutt, 3rd Baron Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
.
Theory

Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
that relates the change in Mach number with the change in stagnation temperature
Stagnation temperature
In thermodynamics and fluid mechanics, stagnation temperature is the temperature at a stagnation point in a fluid flow. At a stagnation point the speed of the fluid is zero and all of the kinetic energy has been converted to internal energy and is added to the local static enthalpy...
, T0. The differential equation is shown below.
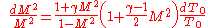
Solving the differential equation leads to the relation shown below, where T0* is the stagnation temperature at the throat location of the duct which is required for thermally choking the flow.
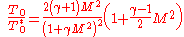
These values are significant in the design of combustion systems. For example, if a turbojet combustion chamber has a maximum temperature of T0* = 2000 K, T0 and M at the entrance to the combustion chamber must be selected so thermal choking does not occur, which will limit the mass flow rate of air into the engine and decrease thrust.
For the Rayleigh flow model, the dimensionless change in entropy relation is shown below.
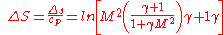
The above equation can be used to plot the Rayleigh line on a Mach number versus ΔS graph, but the dimensionless enthalpy, H, versus ΔS diagram is more often used. The dimensionless enthalpy equation is shown below with an equation relating the static temperature with its value at the choke location for a calorically perfect gas where the heat capacity at constant pressure, cp, remains constant.
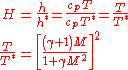
The above equation can be manipulated to solve for M as a function of H. However, due to the form of the T/T* equation, a complicated multi-root relation is formed for M = M(T/T*). Instead, M can be chosen as an independent variable where ΔS and H can be matched up in a chart as shown in Figure 1. Figure 1 shows that heating will increase an upstream, subsonic
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
Mach number until M = 1.0 and the flow chokes
Choked flow
Choked flow is a compressible flow effect. The parameter that becomes "choked" or "limited" is the velocity or the mass flow rate.Choked flow is a fluid dynamic condition associated with the Venturi effect...
. Conversely, adding heat to a duct with an upstream, supersonic
Supersonic
Supersonic speed is a rate of travel of an object that exceeds the speed of sound . For objects traveling in dry air of a temperature of 20 °C this speed is approximately 343 m/s, 1,125 ft/s, 768 mph or 1,235 km/h. Speeds greater than five times the speed of sound are often...
Mach number will cause the Mach number to decrease until the flow chokes. Cooling produces the opposite result for each of those two cases. The Rayleigh flow model reaches maximum entropy at M = 1.0 For subsonic flow, the maximum value of H occurs at M = 0.845. This indicates that cooling, instead of heating, causes the Mach number to move from 0.845 to 1.0 This is not necessarily correct as the stagnation temperature always increases to move the flow from a subsonic Mach number to M = 1, but from M = 0.845 to M = 1.0 the flow accelerates faster than heat is added to it. Therefore, this is a situation where heat is added but T/T* decreases in that region.
Additional Rayleigh Flow Relations

Differential equations can also be developed and solved to describe Rayleigh flow property ratios with respect to the values at the choking location. The ratios for the pressure, density, static temperature, velocity and stagnation pressure are shown below, respectively. They are represented graphically along with the stagnation temperature ratio equation from the previous section. A stagnation property contains a '0' subscript.
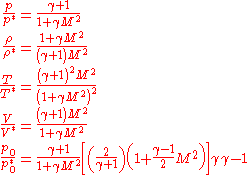
Applications

Dissociation (chemistry)
Dissociation in chemistry and biochemistry is a general process in which ionic compounds separate or split into smaller particles, ions, or radicals, usually in a reversible manner...
of the air-fuel mixture. Producing a shock wave inside the combustion chamber of an engine due to thermal choking is very undesirable due to the decrease in mass flow rate and thrust. Therefore, the Rayleigh flow model is critical for an initial design of the duct geometry and combustion temperature for an engine.
The Rayleigh flow model is also used extensively with the Fanno flow
Fanno flow
Fanno flow refers to adiabatic flow through a constant area duct where the effect of friction is considered. Compressibility effects often come into consideration, although the Fanno flow model certainly also applies to incompressible flow. For this model, the duct area remains constant, the flow...
model. These two models intersect at points on the enthalpy-entropy and Mach number-entropy diagrams, which is meaningful for many applications. However, the entropy values for each model are not equal at the sonic state. The change in entropy is 0 at M = 1 for each model, but the previous statement means the change in entropy from the same arbitrary point to the sonic point is different for the Fanno and Rayleigh flow models. If initial values of si and Mi are defined, a new equation for dimensionless entropy versus Mach number can be defined for each model. These equations are shown below for Fanno and Rayleigh flow, respectively.
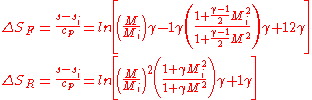
Figure 3 shows the Rayleigh and Fanno lines intersecting with each other for initial conditions of si = 0 and Mi = 3.0 The intersection points are calculated by equating the new dimensionless entropy equations with each other, resulting in the relation below.
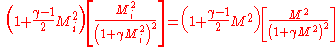
Interestingly, the intersection points occur at the given initial Mach number and its post-normal shock value. For Figure 3, these values are M = 3.0 and 0.4752, which can be found the normal shock tables listed in most compressible flow textbooks. A given flow with a constant duct area can switch between the Rayleigh and Fanno models at these points.
See also
- Fanno flowFanno flowFanno flow refers to adiabatic flow through a constant area duct where the effect of friction is considered. Compressibility effects often come into consideration, although the Fanno flow model certainly also applies to incompressible flow. For this model, the duct area remains constant, the flow...
- Isentropic processIsentropic processIn thermodynamics, an isentropic process or isoentropic process is one in which for purposes of engineering analysis and calculation, one may assume that the process takes place from initiation to completion without an increase or decrease in the entropy of the system, i.e., the entropy of the...
- Isothermal flowIsothermal flowIsothermal flow is a model of compressible fluid flow whereby the flow remains at the same temperature while flowing in a conduit. In the model, heat transferred through the walls of the conduit is offset by frictional heating back into the flow. Although the flow temperature remains constant, a...
- Gas dynamicsGas dynamicsGas dynamics is a branch of fluid dynamics concerned with studying the motion of gases and its consequent effects. Gas dynamics combines the principles of fluid mechanics and thermodynamics...
- Compressible flowCompressible flowCompressible flow is the area of fluid mechanics that deals with fluids in which the fluid density varies significantly in response to a change in pressure. Compressibility effects are typically considered significant if the Mach number of the flow exceeds 0.3, or if the fluid undergoes very large...
- Choked flowChoked flowChoked flow is a compressible flow effect. The parameter that becomes "choked" or "limited" is the velocity or the mass flow rate.Choked flow is a fluid dynamic condition associated with the Venturi effect...
- EnthalpyEnthalpyEnthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
- EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

