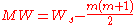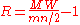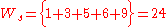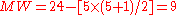Ranklet
Encyclopedia
In statistics
, a ranklet is an orientation-selective non-parametric feature which is based on the computation of Mann–Whitney–Wilcoxon (MWW) rank-sum test statistics. Ranklets achieve similar response to Haar wavelet
s as they share the same pattern of orientation-selectivity, multi-scale nature and a suitable notion of completeness.
Rank-based (non-parametric) features have become popular in the field of image processing
for their robustness in detecting outliers and invariance to monotonic transformations such as brightness, contrast changes and gamma correction
.
The MWW is a combination of Wilcoxon rank-sum test
and Mann–Whitney U-test. It is a non-parametric alternative to the t-test
used to test the hypothesis for the comparison of two independent distributions. It assesses whether two samples of observations, usually referred as Treatment T and Control C, come from the same distribution but do not have to be normally distributed.
The Wilcoxon rank-sum statistics Ws is determined as:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a ranklet is an orientation-selective non-parametric feature which is based on the computation of Mann–Whitney–Wilcoxon (MWW) rank-sum test statistics. Ranklets achieve similar response to Haar wavelet
Haar wavelet
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
s as they share the same pattern of orientation-selectivity, multi-scale nature and a suitable notion of completeness.
Rank-based (non-parametric) features have become popular in the field of image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
for their robustness in detecting outliers and invariance to monotonic transformations such as brightness, contrast changes and gamma correction
Gamma correction
Gamma correction, gamma nonlinearity, gamma encoding, or often simply gamma, is the name of a nonlinear operation used to code and decode luminance or tristimulus values in video or still image systems...
.
The MWW is a combination of Wilcoxon rank-sum test
Wilcoxon signed-rank test
The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used when comparing two related samples or repeated measurements on a single sample to assess whether their population mean ranks differ The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used...
and Mann–Whitney U-test. It is a non-parametric alternative to the t-test
Student's t-test
A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
used to test the hypothesis for the comparison of two independent distributions. It assesses whether two samples of observations, usually referred as Treatment T and Control C, come from the same distribution but do not have to be normally distributed.
The Wilcoxon rank-sum statistics Ws is determined as:
-
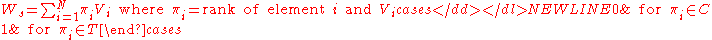
Subsequently, let MW be the Mann–Whitney statistics defined by:
where m is the number of Treatment values.
A ranklet R is defined as the normalization of MW in the range [−1, +1]:
where a positive value means that the Treatment region is brighter than the Control region, and a negative value otherwise.
Example
Suppose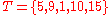 and
and 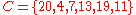 then
then
Intensity 1 4 5 7 9 10 11 13 15 19 20 Sample T C T C T T C C T C C Rank 1 2 3 4 5 6 7 8 9 10 11
Hence, in the above example the Control region was a little bit brighter than the Treatment region.
Method
Since Ranklets are non-linear filters, they can only be applied in the spatial domain. Filtering with Ranklets involves dividing an image window W into Treatment and Control regions as shown in the image below:
Subsequently, Wilcoxon rank-sum test statistics are computed in order to determine the intensity variations among conveniently
chosen regions (according to the required orientation) of the samples in W. The intensity values of both regions are then
replaced by the respective ranking scores. These ranking scores determine a pairwise comparison between the T and C regions. This means that a ranklet essentially counts the number of TxC pairs which are brighter in the T set. Hence a positive value means that the Treatment values are brighter than the Control values, and vice versa.
External links
- MatlabMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
RankletFilter.m -> source file to decompose an image into Intensity Ranklets
-