
Rank 3 permutation group
Encyclopedia
In mathematical finite group theory, a rank 3 permutation group is a group acting transitively on a set such that the stabilizer of a point has 3 orbits. The study of these groups was started by . Several of the sporadic simple groups were discovered as rank 3 permutation groups.
classified the ones such that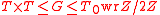 where the socle
where the socle
T of T0 is simple, and T0 is a 2-transitive group of degree √n. classified the ones with a regular elementary abelian normal subgroup classified the ones whose socle is a simple alternating group classified the ones whose socle is a simple classical group classified the ones whose socle is a simple exceptional or sporadic group
Classification
The primitive rank 3 permutation groups are all in one of the following classes:classified the ones such that
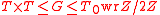 where the socle
where the socleSocle (mathematics)
-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
T of T0 is simple, and T0 is a 2-transitive group of degree √n. classified the ones with a regular elementary abelian normal subgroup classified the ones whose socle is a simple alternating group classified the ones whose socle is a simple classical group classified the ones whose socle is a simple exceptional or sporadic group

