Random walk model of consumption
Encyclopedia
The random walk
model of consumption was introduced by economist Robert Hall
This model uses the Euler equation to model consumption
. He created his consumption theory in response to the Lucas critique
. Using Euler equations to model the random walk of consumption has become the dominant approach to modeling consumption .
to modeling consumption. He incorporated the idea of rational expectations
into his consumption models and sets up the model so that consumers will maximize their utility.
where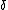
is the subjective time preference rate, 
is the constant interest rate, and 
is the conditional expectation at time period 1.
Assuming that the utility function is quadratic and
, equation will yield
Applying the definition of expectations to equation will give:
where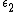
is the innovation term. Equation suggests that consumption is a random walk because consumption is a function of only consumption from the previous period plus the innovation term.
has led some to reject the random walk hypothesis. Some argue that this is due to the model's inability to uncover consumer preference variables such as the intertemporal elasticity of substitution.
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
model of consumption was introduced by economist Robert Hall
Robert Hall (economist)
Robert Ernest "Bob" Hall is an American economist and a Robert and Carole McNeil Senior Fellow at Stanford University's Hoover Institution. He is generally considered a macroeconomist, but he describes himself as an "applied economist"....
This model uses the Euler equation to model consumption
Consumption (economics)
Consumption is a common concept in economics, and gives rise to derived concepts such as consumer debt. Generally, consumption is defined in part by comparison to production. But the precise definition can vary because different schools of economists define production quite differently...
. He created his consumption theory in response to the Lucas critique
Lucas critique
The Lucas critique, named for Robert Lucas′ work on macroeconomic policymaking, argues that it is naïve to try to predict the effects of a change in economic policy entirely on the basis of relationships observed in historical data, especially highly aggregated historical data.The basic idea...
. Using Euler equations to model the random walk of consumption has become the dominant approach to modeling consumption .
Background
Hall introduced his famous random walk model of consumption in 1978. His approach is differentiated from earlier theories by the introduction of the Lucas critiqueLucas critique
The Lucas critique, named for Robert Lucas′ work on macroeconomic policymaking, argues that it is naïve to try to predict the effects of a change in economic policy entirely on the basis of relationships observed in historical data, especially highly aggregated historical data.The basic idea...
to modeling consumption. He incorporated the idea of rational expectations
Rational expectations
Rational expectations is a hypothesis in economics which states that agents' predictions of the future value of economically relevant variables are not systematically wrong in that all errors are random. An alternative formulation is that rational expectations are model-consistent expectations, in...
into his consumption models and sets up the model so that consumers will maximize their utility.
Model
Consider a two-period case. The Euler equation for this model iswhere
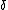is the subjective time preference rate, is the constant interest rate, and is the conditional expectation at time period 1.Assuming that the utility function is quadratic and
, equation will yieldApplying the definition of expectations to equation will give:
where
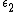is the innovation term. Equation suggests that consumption is a random walk because consumption is a function of only consumption from the previous period plus the innovation term.Advantages
Use of the Euler equations to estimate consumption appears to have advantages over traditional models. First, using Euler equations is simpler than conventional methods. This avoids the need to solve the consumer's optimization problem and is the most appeal element of using Euler equations to some economists.Criticisms
Controversy has arisen over using Euler equations to model consumption. Applying the Euler consumption equations has trouble explaining empirical data. Attempting to use to Euler equations to model consumption in the United StatesUnited States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
has led some to reject the random walk hypothesis. Some argue that this is due to the model's inability to uncover consumer preference variables such as the intertemporal elasticity of substitution.