Rand index
Encyclopedia
The Rand index or Rand measure (named after William M. Rand) in statistics
, and in particular in data clustering
, is a measure of the similarity between two data clustering
s. The adjusted-for-chance form of the Rand index is the adjusted Rand index.
elements 
and two partitions
of
to compare, 
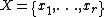and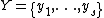 
, the following is defined:
The Rand index,
, is:
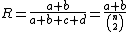
Intuitively,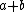
can be considered as the number of agreements between 
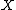and 
and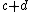 
as the number of disagreements between 
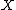and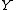 
.
In mathematical terms, a, b, c, d are defined as follows:
for some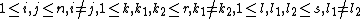
.
of 
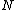data points and two groupings (e.g. clusterings) of these points, namely 
and 
, the overlappings between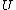 
and 
can be summarized in a contingency table where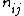 
denotes the number of common objects of groups 
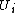and 
: 
.
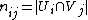, more specifically
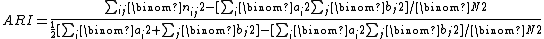
where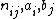
are values from the contingency table.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, and in particular in data clustering
Data clustering
Cluster analysis or clustering is the task of assigning a set of objects into groups so that the objects in the same cluster are more similar to each other than to those in other clusters....
, is a measure of the similarity between two data clustering
Data clustering
Cluster analysis or clustering is the task of assigning a set of objects into groups so that the objects in the same cluster are more similar to each other than to those in other clusters....
s. The adjusted-for-chance form of the Rand index is the adjusted Rand index.
Definition
Given a set of elements and two partitionsPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of
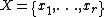to compare, and 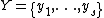, the following is defined:
-
, the number of pairs of elements in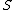 
that are in the same set in 
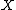and in the same set in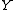 
-
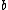, the number of pairs of elements in 
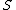that are in different sets in 
and in different sets in 
-
, the number of pairs of elements in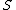 
that are in the same set in 
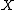and in different sets in 
-
, the number of pairs of elements in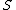 
that are in different sets in 
and in the same set in 
The Rand index,
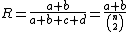
, is:Intuitively,
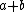can be considered as the number of agreements between 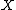and and 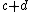as the number of disagreements between 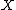and 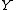.Properties
The Rand index has a value between 0 and 1, with 0 indicating that the two data clusters do not agree on any pair of points and 1 indicating that the data clusters are exactly the same.In mathematical terms, a, b, c, d are defined as follows:
, where 
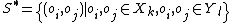
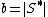, where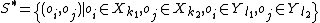 
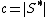, where 
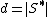, where 
for some
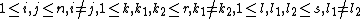.Adjusted Rand index
The adjusted Rand index is the corrected-for-chance version of the Rand index.The contingency table
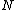Given a set of data points and two groupings (e.g. clusterings) of these points, namely and , the overlappings between 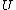and can be summarized in a contingency table where 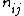denotes the number of common objects of groups 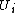and : .
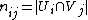| U\V |  |
 |
 |
 |
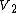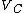Sums |
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
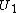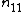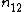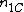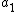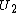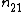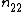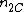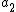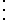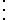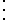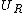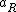| Sums |  |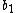
 |
 |
 |
|
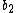Definition
The adjusted form of the Rand Index, the Adjusted Rand Index, is, more specifically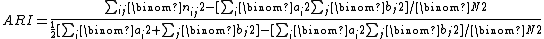where
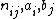are values from the contingency table.