
Ragsdale conjecture
Encyclopedia
The Ragsdale conjecture is a mathematical
conjecture
that concerns the possible arrangements of real algebraic curves embedded in the projective plane
. It was proposed by Virginia Ragsdale
several years after 1900 and was disproved in 1979.
, which was proposed in the year 1900, along with 22 other unsolved problems of the 19th century
. Ragsdale conjectured a particular upper bound on the number of topological circles of a certain type, along with the basis of evidence. The conjecture was held of high importance in the field of real algebraic geometry for nearly a century. Later Oleg Viro
and Ilya Itenberg produced counterexamples to the Ragsdale conjecture, although the problem of finding a sharp upper bound remains unsolved.
Assume that an algebraic curve
of degree 2k contains p even and n odd ovals. Ragsdale conjectured that
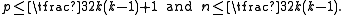
She also posed the inequality
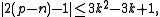
and showed that the inequality could not be further improved. This inequality was later proved by Petrovsky
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
that concerns the possible arrangements of real algebraic curves embedded in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. It was proposed by Virginia Ragsdale
Virginia Ragsdale
Virginia Ragsdale was a teacher and a mathematician specializing in number theory. She is most known as the creator of the Ragsdale conjecture.-Early life:Ragsdale was born on a farm in Jamestown, North Carolina...
several years after 1900 and was disproved in 1979.
Background
Her dissertation dealt with Hilbert's sixteenth problemHilbert's sixteenth problem
Hilbert's 16th problem was posed by David Hilbert at the Paris conference of the International Congress of Mathematicians in 1900, together with the other 22 problems....
, which was proposed in the year 1900, along with 22 other unsolved problems of the 19th century
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
. Ragsdale conjectured a particular upper bound on the number of topological circles of a certain type, along with the basis of evidence. The conjecture was held of high importance in the field of real algebraic geometry for nearly a century. Later Oleg Viro
Oleg Viro
Oleg Viro is a mathematician in the fields of topology and algebraic geometry, most notably real algebraic geometry, tropical geometry and knot theory....
and Ilya Itenberg produced counterexamples to the Ragsdale conjecture, although the problem of finding a sharp upper bound remains unsolved.
Conjecture
Ragsdale's main conjecture is as follows.Assume that an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree 2k contains p even and n odd ovals. Ragsdale conjectured that
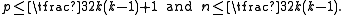
She also posed the inequality
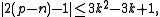
and showed that the inequality could not be further improved. This inequality was later proved by Petrovsky
Ivan Petrovsky
Ivan Georgievich Petrovsky, also Petrovskii was a Soviet mathematician in the field of partial differential equations, and studied Petrovsky lacunas. He greatly contributed to solution of Hilbert's 19th and 16th problems...
.

