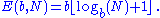Radix economy
Encyclopedia
Various proposals have been made to quantify the relative costs between using different radices
in representing numbers, especially in computer systems.
The radix economy measures the cost of storing or transmitting the number N in base b if the cost of each "digit" is proportional to b. A base with a lower average radix economy is therefore, in some senses, more efficient than a base with a higher average radix economy.
For example, 100
in decimal
has three digits, so its radix economy is 10×3 = 30; its binary respresentation has seven digits (11001002) so it has radix economy 2×7 = 14 in base 2; in base 3 its representation has five digits (102013) with a radix economy of 3×5 = 15; in base 36 (2S36) its radix economy is 36×2 = 72.
The radix economy of bases b1 and b2 may be compared for a large fixed value of N:
Since the function
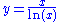
is strictly decreasing on 0 < x < e and strictly increasing on x > e, its minimum is at e
, which is therefore the base with the lowest average radix economy. Since 2 / ln(2) ≈ 2.89 and 3 / ln(3) ≈ 2.73, it follows that 3 is the integer base with the lowest average radix economy.
The average radix economy of the integers from 1 to 100 in various bases is:
composed of several triode
s. Whether vacuum tube
s or thyratron
s, the triodes were the most expensive part of a counter. For small radices r less than about 7, a single digit required r triodes. (Larger radices required 2r triodes arranged as r flip-flop
s, as in ENIAC
's decimal counters.)
So the number of triodes in a numerical register with n digits was rn. In order to represent numbers up to 106, the following numbers of tubes were needed:
The authors conclude,
A similar analysis suggests that the optimum design of a large telephone menu system
to minimise the number of menu choices that a customer must listen to (i.e. the product of the number of choices per menu and the number of menu levels) is to have three choices per menu.
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
in representing numbers, especially in computer systems.
Definition
The radix economy E(b,N) for any particular number N in a given base b is equal to the number of digits needed to express it in that base, multiplied by the radix:The radix economy measures the cost of storing or transmitting the number N in base b if the cost of each "digit" is proportional to b. A base with a lower average radix economy is therefore, in some senses, more efficient than a base with a higher average radix economy.
For example, 100
100 (number)
100 is the natural number following 99 and preceding 101.-In mathematics:One hundred is the square of 10...
in decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
has three digits, so its radix economy is 10×3 = 30; its binary respresentation has seven digits (11001002) so it has radix economy 2×7 = 14 in base 2; in base 3 its representation has five digits (102013) with a radix economy of 3×5 = 15; in base 36 (2S36) its radix economy is 36×2 = 72.
The radix economy of bases b1 and b2 may be compared for a large fixed value of N:
Since the function
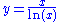
is strictly decreasing on 0 < x < e and strictly increasing on x > e, its minimum is at e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, which is therefore the base with the lowest average radix economy. Since 2 / ln(2) ≈ 2.89 and 3 / ln(3) ≈ 2.73, it follows that 3 is the integer base with the lowest average radix economy.
The average radix economy of the integers from 1 to 100 in various bases is:
| Base b | Average of E(b,N) for N=1 to 100 |
|---|---|
| 2 | 11.6 |
| e | 11.33524 |
| 3 | 11.52 |
| 4 | 12.76 |
| 10 | 19.2 |
Radix times required digits
The classic 1950 reference High-Speed Computing Devices describes a particular situation using contemporary technology. Each digit of a number would be stored as the state of a ring counterRing counter
A ring counter is a type of counter composed of a circular shift register. The output of the last shift register is fed to the input of the first register.There are two types of ring counters:...
composed of several triode
Triode
A triode is an electronic amplification device having three active electrodes. The term most commonly applies to a vacuum tube with three elements: the filament or cathode, the grid, and the plate or anode. The triode vacuum tube was the first electronic amplification device...
s. Whether vacuum tube
Vacuum tube
In electronics, a vacuum tube, electron tube , or thermionic valve , reduced to simply "tube" or "valve" in everyday parlance, is a device that relies on the flow of electric current through a vacuum...
s or thyratron
Thyratron
A thyratron is a type of gas filled tube used as a high energy electrical switch and controlled rectifier. Triode, tetrode and pentode variations of the thyratron have been manufactured in the past, though most are of the triode design...
s, the triodes were the most expensive part of a counter. For small radices r less than about 7, a single digit required r triodes. (Larger radices required 2r triodes arranged as r flip-flop
Flip-flop
Flip-flops, thongs, Japanese sandals, or jandals are an open type of outdoor footwear, consisting of a flat sole held loosely on the foot by a Y-shaped strap, like a thin thong, that passes between the first and second toes and around either side of the foot...
s, as in ENIAC
ENIAC
ENIAC was the first general-purpose electronic computer. It was a Turing-complete digital computer capable of being reprogrammed to solve a full range of computing problems....
's decimal counters.)
So the number of triodes in a numerical register with n digits was rn. In order to represent numbers up to 106, the following numbers of tubes were needed:
| Radix r | Tubes N = rn |
|---|---|
| 2 | 39.20 |
| 3 | 38.24 |
| 4 | 39.20 |
| 5 | 42.90 |
| 10 | 60.00 |
The authors conclude,
A similar analysis suggests that the optimum design of a large telephone menu system
Interactive voice response
Interactive voice response is a technology that allows a computer to interact with humans through the use of voice and DTMF keypad inputs....
to minimise the number of menu choices that a customer must listen to (i.e. the product of the number of choices per menu and the number of menu levels) is to have three choices per menu.
Other criteria
In another application, the authors of High-Speed Computing Devices consider the speed with which an encoded number may be sent as a series of high-frequency voltage pulses. For this application the compactness of the representation is more important than in the above storage example. They conclude, "A saving of 58 per cent can be gained in going from a binary to a ternary system. A smaller percentage gain is realized in going from a radix 3 to a radix 4 system."Further reading
- S.L. Hurst, "Multiple-Valued Logic-Its Status and its Future", IEEE trans. computers, Vol. C-33, No 12, pp. 1160–1179, DEC 1984.
- J. T. Butler, "Multiple-Valued Logic in VLSI Design, ” IEEE Computer Society Press Technology Series, 1991.
- C.M. Allen, D.D. Givone “The Allen-Givone Implementation Oriented Algebra", in Computer Science and Multiple-Valued Logic: Theory and Applications, D.C. Rine, second edition, D.C. Rine, ed., The Elsevier North-Holland, New York, N.Y., 1984. pp. 268–288.
- G. Abraham, "Multiple-Valued Negative Resistance Integrated Circuits", in Computer Science and Multiple-Valued Logic: Theory and Applications, D.C. Rine, second edition, D.C. Rine, ed., The Elsevier North-Holland, New York, N.Y., 1984. pp. 394–446.