Quasi-category
Encyclopedia
In mathematics, a quasi-category (also called quasicategory, weak Kan complex, inner Kan complex, infinity category, ∞-category, Boardman complex, quategory) is a higher categorical generalization of a notion of a category introduced by .
André Joyal
has much advanced the study of quasi-categories showing that most of the usual basic category theory
and some of the advanced notions and theorems have their analogues for quasi-categories. An elaborate treatise of the theory of quasi-categories has been expounded by .
The idea of higher category theory (at least, higher category theory when higher morphisms are invertible) is that, as opposed to the standard notion of a category
, there should be a mapping space (rather than a mapping set) between two objects. This suggests that a higher category should simply be a topologically enriched category. The model of quasi-categories is, however, better suited to applications than that of topologically enriched categories, though it has been proved by Lurie that the two have natural model structures that are Quillen equivalent.
satisfying the inner Kan conditions (also called weak Kan condition): every inner horn in C, namely a map of simplicial sets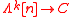
where 
, has a filler, that is, an extension to a map 
.
The idea is that 2-simplices $\Delta[2] \to C$ are supposed to represent commutative triangles (at least up to homotopy). A map $\Lambda^1[2] \to C$ represents a composable pair. Thus, in a quasi-category, one cannot define a composition law on morphisms, since one can choose many ways to compose maps.
One (non-obvious) consequence of the definition is that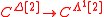
is a trivial Kan fibration. In other words, while the composition law is not uniquely defined, it is unique up to a contractible choice.
The homotopy category has objects as the vertices of C. The morphisms are given by homotopy classes of edges between vertices. Composition is given using the horn filler condition for n=2.
André Joyal
André Joyal
André Joyal is a professor of mathematics at the Université du Québec à Montréal who works on category theory. Joyal was born in Drummondville . He has three children and lives in Montreal.- Main research :...
has much advanced the study of quasi-categories showing that most of the usual basic category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
and some of the advanced notions and theorems have their analogues for quasi-categories. An elaborate treatise of the theory of quasi-categories has been expounded by .
The idea of higher category theory (at least, higher category theory when higher morphisms are invertible) is that, as opposed to the standard notion of a category
Category
Category, plural categories, may refer to:-Philosophy:*Category of being*Categories *Category *Categories *Category *Stoic Categories-Mathematics:* Category * Abelian category...
, there should be a mapping space (rather than a mapping set) between two objects. This suggests that a higher category should simply be a topologically enriched category. The model of quasi-categories is, however, better suited to applications than that of topologically enriched categories, though it has been proved by Lurie that the two have natural model structures that are Quillen equivalent.
Definition
By the definition, a quasi-category C is a simplicial setSimplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
satisfying the inner Kan conditions (also called weak Kan condition): every inner horn in C, namely a map of simplicial sets
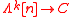where , has a filler, that is, an extension to a map .The idea is that 2-simplices $\Delta[2] \to C$ are supposed to represent commutative triangles (at least up to homotopy). A map $\Lambda^1[2] \to C$ represents a composable pair. Thus, in a quasi-category, one cannot define a composition law on morphisms, since one can choose many ways to compose maps.
One (non-obvious) consequence of the definition is that
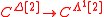is a trivial Kan fibration. In other words, while the composition law is not uniquely defined, it is unique up to a contractible choice.The homotopy category
Given a quasi-category C, one can associate to it an ordinary category hC, called the homotopy category.The homotopy category has objects as the vertices of C. The morphisms are given by homotopy classes of edges between vertices. Composition is given using the horn filler condition for n=2.
Examples
- The nerve of a category is a quasi-category with the extra property that the filling of any inner horn is unique. Conversely a quasi-category such that any inner horn has a unique filling is isomorphic to the nerve of some category.
- Every Kan complex is an example of a quasi-category. The difference here is that maps from all horns——not just inner ones——can be filled.
External links
- Joyal's Catlab entry: The theory of quasi-categories
- nlab entry: quasi-category