Quantum register
Encyclopedia
A quantum register is the quantum mechanical
analogue of a classical processor register
.
A mathematical description of a quantum register is achieved by using a tensor product
of qubit
bra
or ket
vectors. For example, an n qubit quantum register is described by an element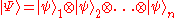
in the tensor product Hilbert space
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
analogue of a classical processor register
Processor register
In computer architecture, a processor register is a small amount of storage available as part of a CPU or other digital processor. Such registers are addressed by mechanisms other than main memory and can be accessed more quickly...
.
A mathematical description of a quantum register is achieved by using a tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
bra
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
or ket
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
vectors. For example, an n qubit quantum register is described by an element
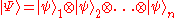in the tensor product Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...