Quantum programming
Encyclopedia
Quantum programming is a set of computer programming language
s that allow the expression of quantum algorithm
s using high-level constructs. The point of quantum languages is not so much to provide a tool for programmers, but to provide tools for researchers to understand better how quantum computation works and how to formally reason about quantum algorithms.
Efforts are underway to develop functional programming languages for quantum computing. Examples include Selinger's QPL , and the Haskell-like
language QML by Altenkirch and Grattage . Higher-order quantum programming languages, based on lambda calculus
, have been proposed by van Tonder , Selinger and Valiron and by Arrighi and Dowek.
Simon Gay's Quantum Programming Languages Survey has more information on the current state of research and a comprehensive bibliography of resources.
s was introduced and, moreover, it was tightly connected with a model of quantum machine called Quantum Random Access Machine (QRAM).
resembles syntax of the C programming language and classical data type
s are similar to data types in C. You can combine a classical code and a quantum code in one source code.
The basic built-in quantum data type in QCL is the qureg (quantum register). It can be interpreted as an array of qubits (quantum bits).
qureg x1[2]; // 2-qubit quantum register x1
qureg x2[2]; // 2-qubit quantum register x2
H(x1); // Hadamard operation on x1
H(x2[1]); // Hadamard operation on the first qubit of the register x2
Since the qcl interpreter uses qlib simulation library, it is possible to observe the internal state of the quantum machine during execution of the quantum program.
qcl> dump
: STATE: 4 / 32 qubits allocated, 28 / 32 qubits free
0.35355 |0> + 0.35355 |1> + 0.35355 |2> + 0.35355 |3>
+ 0.35355 |8> + 0.35355 |9> + 0.35355 |10> + 0.35355 |11>
Note that the dump operation is different from measurement, since it does not influence the state of the quantum machine and can be realised only using a simulator.
The QCL standard library provides standard quantum operators used in quantum algorithms such as:
But the most important feature of QCL is the support for user-defined operators and functions. Like in modern programming languages, it is possible to define new operations which can be used to manipulate quantum data. For example:
operator diffuse (qureg q) {
H(q); // Hadamard Transform
Not(q); // Invert q
CPhase(pi, q); // Rotate if q=1111..
!Not(q); // undo inversion
!H(q); // undo Hadamard Transform
}
defines inverse about the mean operator used in Grover's algorithm
. This allows one to define algorithms on a higher level of abstraction and extend the library of functions available for programmers.
Q Language was implemented as an extension of C++ programming language. It
provides classes for basic quantum operations like QHadamard,
QFourier, QNot, and QSwap, which are derived from the base class Qop.
New operators can be defined using C++ class mechanism.
Quantum memory is represented by class Qreg.
Qreg x1; // 1-qubit quantum register with initial value 0
Qreg x2(2,0); // 2-qubit quantum register with initial value 0
Computation process is executed using provided simulator. Noisy environment can be
simulated using parameters of the simulator.
created by Edsger Dijkstra
.
It can be described as a language of quantum programmes specification.
paradigm were proposed. Functional programming languages are well-suited for reasoning about programs.
superoperator
s.
-like quantum programming language by Altenkirch and Grattage. Unlike Selinger's QPL, this language takes duplication, rather than discarding, of quantum information as a primitive operation. Duplication in this context is understood to be the operation that maps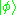
to 
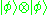, and is not to be confused with the impossible operation of cloning
; the authors claim it is akin to how sharing is modelled in classical languages. QML also introduces both classical and
quantum control operators, whereas most other languages rely on classical control.
An operational semantics
for QML is given in terms of quantum circuit
s, while a denotational semantics
is presented in terms of superoperator
s, and these are shown to agree. Both the operational and denotational semantics have been implemented (classically) in Haskell.
, introduced by Alonzo Church
and Stephen Cole Kleene
in the 1930s. The purpose of quantum lambda calculi is to extend quantum programming languages with a theory of higher-order functions.
The first attempt to define a quantum lambda calculus was made by Philip Maymin in 1996.
His lambda-q calculus is powerful enough to express any quantum computation. However, this language can efficiently solve NP-complete
problems, and therefore appears to be strictly stronger than the standard quantum computational models (such as the quantum Turing machine
or the quantum circuit
model). Therefore, Maymin's lambda-q calculus is probably not implementable on a physical device.
In 2003, André van Tonder defined an extension of the lambda calculus
suitable for proving correctness of quantum programs. He also provided an implementation in the Scheme programming language.
In 2004, Selinger and Valiron defined a strongly typed lambda calculus for quantum computation with a type system based on linear logic
.
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s that allow the expression of quantum algorithm
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
s using high-level constructs. The point of quantum languages is not so much to provide a tool for programmers, but to provide tools for researchers to understand better how quantum computation works and how to formally reason about quantum algorithms.
Efforts are underway to develop functional programming languages for quantum computing. Examples include Selinger's QPL , and the Haskell-like
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
language QML by Altenkirch and Grattage . Higher-order quantum programming languages, based on lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, have been proposed by van Tonder , Selinger and Valiron and by Arrighi and Dowek.
Simon Gay's Quantum Programming Languages Survey has more information on the current state of research and a comprehensive bibliography of resources.
Quantum pseudocode
Quantum pseudocode proposed by E. Knill is the first formalised language for description of quantum algorithmQuantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
s was introduced and, moreover, it was tightly connected with a model of quantum machine called Quantum Random Access Machine (QRAM).
Quantum computing language
QCL (Quantum Computer Language) is one of the first implemented quantum programming languages. Its syntaxSyntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
resembles syntax of the C programming language and classical data type
Data type
In computer programming, a data type is a classification identifying one of various types of data, such as floating-point, integer, or Boolean, that determines the possible values for that type; the operations that can be done on values of that type; the meaning of the data; and the way values of...
s are similar to data types in C. You can combine a classical code and a quantum code in one source code.
The basic built-in quantum data type in QCL is the qureg (quantum register). It can be interpreted as an array of qubits (quantum bits).
qureg x1[2]; // 2-qubit quantum register x1
qureg x2[2]; // 2-qubit quantum register x2
H(x1); // Hadamard operation on x1
H(x2[1]); // Hadamard operation on the first qubit of the register x2
Since the qcl interpreter uses qlib simulation library, it is possible to observe the internal state of the quantum machine during execution of the quantum program.
qcl> dump
: STATE: 4 / 32 qubits allocated, 28 / 32 qubits free
0.35355 |0> + 0.35355 |1> + 0.35355 |2> + 0.35355 |3>
+ 0.35355 |8> + 0.35355 |9> + 0.35355 |10> + 0.35355 |11>
Note that the dump operation is different from measurement, since it does not influence the state of the quantum machine and can be realised only using a simulator.
The QCL standard library provides standard quantum operators used in quantum algorithms such as:
- controlled-not with many target qubits,
- Hadamard operation on many qubits,
- parse and controlled phase.
But the most important feature of QCL is the support for user-defined operators and functions. Like in modern programming languages, it is possible to define new operations which can be used to manipulate quantum data. For example:
operator diffuse (qureg q) {
H(q); // Hadamard Transform
Not(q); // Invert q
CPhase(pi, q); // Rotate if q=1111..
!Not(q); // undo inversion
!H(q); // undo Hadamard Transform
}
defines inverse about the mean operator used in Grover's algorithm
Grover's algorithm
Grover's algorithm is a quantum algorithm for searching an unsorted database with N entries in O time and using O storage space . It was invented by Lov Grover in 1996....
. This allows one to define algorithms on a higher level of abstraction and extend the library of functions available for programmers.
Syntax
- Data types
- Quantum - qureg, quvoid, quconst, quscratch, qucond
- Classical - int, real, complex, boolean, string, vector, matrix, tensor
- Function types
- qufunct - Pseudo-classic operators. Can only change the permutation of basic states.
- operator - General unitary operators. Can change the amplitude.
- procedure - Can call measure, print, and dump inside this function. This function is non-invertible.
- Build-in functions
- Quantum
- qufunct - Fanout, Swap, Perm2, Perm4, Perm8, Not, CNot
- operator - Matrix2x2, Matrix4x4, Matrix8x8, Rot, Mix, H, CPhase, SqrtNot, X, Y, Z, S, T
- procedure - measure, dump, reset
- Classical
- Arithmetic - sin, cos, tan, log, sqrt, ...
- Complex - Re, Im, conj
- Quantum
Q language
Q Language is the second implemented imperative quantum programming language.Q Language was implemented as an extension of C++ programming language. It
provides classes for basic quantum operations like QHadamard,
QFourier, QNot, and QSwap, which are derived from the base class Qop.
New operators can be defined using C++ class mechanism.
Quantum memory is represented by class Qreg.
Qreg x1; // 1-qubit quantum register with initial value 0
Qreg x2(2,0); // 2-qubit quantum register with initial value 0
Computation process is executed using provided simulator. Noisy environment can be
simulated using parameters of the simulator.
qGCL
Quantum Guarded Command Language (qGCL) was defined by P. Zuliani in his PhD thesis. It is based on Guarded Command LanguageGuarded Command Language
The Guarded Command Language is a language defined by Edsger Dijkstra for predicate transformer semantics. It combines programming concepts in a compact way, before the program is written in some practical programming language...
created by Edsger Dijkstra
Edsger Dijkstra
Edsger Wybe Dijkstra ; ) was a Dutch computer scientist. He received the 1972 Turing Award for fundamental contributions to developing programming languages, and was the Schlumberger Centennial Chair of Computer Sciences at The University of Texas at Austin from 1984 until 2000.Shortly before his...
.
It can be described as a language of quantum programmes specification.
Functional quantum programming languages
During the last few years many quantum programming languages based on the functional programmingFunctional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
paradigm were proposed. Functional programming languages are well-suited for reasoning about programs.
QFC and QPL
QFC and QPL are two closely related quantum programming languages defined by Peter Selinger. They differ only in their syntax: QFC uses a flow chart syntax, whereas QPL uses a textual syntax. These languages have classical control flow, but can operate on quantum or classical data. Selinger gives a denotational semantics for these languages in a category ofsuperoperator
Superoperator
In physics, a superoperator is a linear operator acting on a vector space of linear operators.Sometimes the term refers more specially to a completely positive map which does not increase or preserves the trace of its argument....
s.
QML
QML is a HaskellHaskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
-like quantum programming language by Altenkirch and Grattage. Unlike Selinger's QPL, this language takes duplication, rather than discarding, of quantum information as a primitive operation. Duplication in this context is understood to be the operation that maps
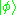to 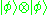, and is not to be confused with the impossible operation of cloningNo cloning theorem
The no-cloning theorem is a result of quantum mechanics that forbids the creation of identical copies of an arbitrary unknown quantum state. It was stated by Wootters, Zurek, and Dieks in 1982, and has profound implications in quantum computing and related fields.The state of one system can be...
; the authors claim it is akin to how sharing is modelled in classical languages. QML also introduces both classical and
quantum control operators, whereas most other languages rely on classical control.
An operational semantics
Operational semantics
In computer science, operational semantics is a way to give meaning to computer programs in a mathematically rigorous way. Operational semantics are classified into two categories: structural operational semantics formally describe how the individual steps of a computation take place in a...
for QML is given in terms of quantum circuit
Quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
s, while a denotational semantics
Denotational semantics
In computer science, denotational semantics is an approach to formalizing the meanings of programming languages by constructing mathematical objects which describe the meanings of expressions from the languages...
is presented in terms of superoperator
Superoperator
In physics, a superoperator is a linear operator acting on a vector space of linear operators.Sometimes the term refers more specially to a completely positive map which does not increase or preserves the trace of its argument....
s, and these are shown to agree. Both the operational and denotational semantics have been implemented (classically) in Haskell.
Quantum lambda calculi
Quantum lambda calculi are extensions of the lambda calculusLambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, introduced by Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
and Stephen Cole Kleene
Stephen Cole Kleene
Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
in the 1930s. The purpose of quantum lambda calculi is to extend quantum programming languages with a theory of higher-order functions.
The first attempt to define a quantum lambda calculus was made by Philip Maymin in 1996.
His lambda-q calculus is powerful enough to express any quantum computation. However, this language can efficiently solve NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problems, and therefore appears to be strictly stronger than the standard quantum computational models (such as the quantum Turing machine
Quantum Turing machine
A quantum Turing machine , also a universal quantum computer, is an abstract machine used to model the effect of a quantum computer. It provides a very simple model which captures all of the power of quantum computation. Any quantum algorithm can be expressed formally as a particular quantum...
or the quantum circuit
Quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
model). Therefore, Maymin's lambda-q calculus is probably not implementable on a physical device.
In 2003, André van Tonder defined an extension of the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
suitable for proving correctness of quantum programs. He also provided an implementation in the Scheme programming language.
In 2004, Selinger and Valiron defined a strongly typed lambda calculus for quantum computation with a type system based on linear logic
Linear logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
.
External links
- 5th International Workshop on Quantum Physics and Logic
- 4th International Workshop on Quantum Programming Languages
- 3rd International Workshop on Quantum Programming Languages
- 2nd International Workshop on Quantum Programming Languages
- Bibliography on Quantum Programming Languages
- Quantum programming language in Quantiki