Quantum field theory in curved spacetime
Encyclopedia
Quantum field theory in curved spacetime is an extension of standard, Minkowski-space quantum field theory
to curved spacetime
. A general prediction of this theory is that particles can be created by time dependent gravitational fields (multigraviton pair production), or by time independent gravitational fields that contain horizons.
Thanks to the equivalence principle
the quantization procedure locally resembles that of normal coordinates
where the affine connection
at the origin is set to zero and a nonzero Riemann tensor in general once the proper (covariant) formalism is chosen; however, interesting new phenomena occur. Even in flat spacetime quantum field theory, the number of particles is not well-defined locally. For non-zero cosmological constant
s, on curved spacetimes quantum fields lose their interpretation as asymptotic particle
s. Only in certain situations, such as in asymptotically flat spacetimes (zero cosmological curvature), can the notion of incoming and outgoing particle be recovered, thus enabling one to define an S-matrix. Even then, as in flat spacetime, the asymptotic particle interpretation depends on the observer (i.e., different observers may measure different numbers of asymptotic particles on a given spacetime).
Another observation is that unless the background metric has a global timelike Killing vector, there is no way way to define a vacuum or ground state canonically. The concept of a vacuum is not invariant under diffeomorphism
s. This is because a mode decomposition of a field into positive and negative frequency modes is not invariant under diffeomorphisms. If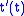
is a diffeomorphism, in general, the Fourier transform of 
will contain negative frequencies even if 
. Creation operators correspond to positive frequencies, while annihilation operators correspond to negative frequencies. This is why a state which looks like a vacuum to one observer can look like a heat bath to another accelerating with respect to the former observer.
The most striking application of the theory is Hawking
's prediction that Schwarzschild black holes radiate with a thermal spectrum
. A related prediction is the Unruh effect
: accelerated observers in the vacuum measure a thermal bath of particles.
This formalism is also used to predict the primordial density perturbation spectrum arising from cosmic inflation
, i.e. the Bunch–Davies vacuum. Since this spectrum is measured by a variety of cosmological
measurements—such as the CMB
-- if inflation is correct this particular prediction of the theory has already been verified.
The theory of quantum field theory in curved spacetime can be considered as a first approximation to quantum gravity
. A second step towards that theory would be semiclassical gravity
, which would include the influence of particles created by a strong gravitational field on the spacetime (which is still considered classical and the equivalence principle still holds).
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
to curved spacetime
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. A general prediction of this theory is that particles can be created by time dependent gravitational fields (multigraviton pair production), or by time independent gravitational fields that contain horizons.
Thanks to the equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
the quantization procedure locally resembles that of normal coordinates
Normal coordinates
In differential geometry, normal coordinates at a point p in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of p obtained by applying the exponential map to the tangent space at p...
where the affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
at the origin is set to zero and a nonzero Riemann tensor in general once the proper (covariant) formalism is chosen; however, interesting new phenomena occur. Even in flat spacetime quantum field theory, the number of particles is not well-defined locally. For non-zero cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
s, on curved spacetimes quantum fields lose their interpretation as asymptotic particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s. Only in certain situations, such as in asymptotically flat spacetimes (zero cosmological curvature), can the notion of incoming and outgoing particle be recovered, thus enabling one to define an S-matrix. Even then, as in flat spacetime, the asymptotic particle interpretation depends on the observer (i.e., different observers may measure different numbers of asymptotic particles on a given spacetime).
Another observation is that unless the background metric has a global timelike Killing vector, there is no way way to define a vacuum or ground state canonically. The concept of a vacuum is not invariant under diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s. This is because a mode decomposition of a field into positive and negative frequency modes is not invariant under diffeomorphisms. If
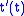is a diffeomorphism, in general, the Fourier transform of will contain negative frequencies even if . Creation operators correspond to positive frequencies, while annihilation operators correspond to negative frequencies. This is why a state which looks like a vacuum to one observer can look like a heat bath to another accelerating with respect to the former observer.The most striking application of the theory is Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
's prediction that Schwarzschild black holes radiate with a thermal spectrum
Hawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
. A related prediction is the Unruh effect
Unruh effect
The Unruh effect , was first described by Stephen Fulling in 1973, Paul Davies in 1975 and Bill Unruh in 1976. It is the prediction that an accelerating observer will observe black-body radiation where an inertial observer would observe none...
: accelerated observers in the vacuum measure a thermal bath of particles.
This formalism is also used to predict the primordial density perturbation spectrum arising from cosmic inflation
Cosmic inflation
In physical cosmology, cosmic inflation, cosmological inflation or just inflation is the theorized extremely rapid exponential expansion of the early universe by a factor of at least 1078 in volume, driven by a negative-pressure vacuum energy density. The inflationary epoch comprises the first part...
, i.e. the Bunch–Davies vacuum. Since this spectrum is measured by a variety of cosmological
Cosmology
Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
measurements—such as the CMB
CMB
CMB can mean:*The IATA airport code for Bandaranaike International Airport, Colombo – Sri Lanka's only international airport*C.M.B., the debut album of American R&B and pop group Color Me Badd...
-- if inflation is correct this particular prediction of the theory has already been verified.
The theory of quantum field theory in curved spacetime can be considered as a first approximation to quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
. A second step towards that theory would be semiclassical gravity
Semiclassical gravity
Semiclassical gravity is the approximation to the theory of quantum gravity in which one treats matter fields as being quantum and the gravitational field as being classical....
, which would include the influence of particles created by a strong gravitational field on the spacetime (which is still considered classical and the equivalence principle still holds).
Suggested reading
- R.M. Wald. Quantum field theory in curved space-time and black hole thermodynamics. Chicago U. (1995).
- S.A. Fulling. Aspects of quantum field theory in curved space-time. CUP (1989).
- N.D. Birrell & P.C.W. Davies. Quantum fields in curved space. CUP (1982).
- L. H. Ford Quantum Field Theory in Curved Spacetime (1997).
- V.Mukhanov and S.Winitzki. Introduction to Quantum Effects in Gravity. CUP (2007).
- T. Jacobson Introduction to Quantum Fields in Curved Spacetime and the Hawking Effect (2004).
- L. Parker & D. Toms. Quantum Field Theory in Curved Spacetime. (2009).