
Quadratic residue code
Encyclopedia
A quadratic residue code is a type of cyclic code.
There is a quadratic residue code of length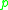
over the finite field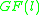 whenever
whenever 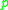
and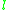 are primes,
are primes,  is odd and
is odd and
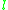 is a quadratic residue modulo
is a quadratic residue modulo 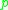 .
.
Its generator polynomial as a cyclic code is given by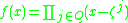
where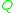 is the set of quadratic residues of
is the set of quadratic residues of
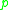 in the set
in the set 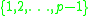 and
and
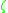 is a primitive
is a primitive 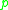 th root of
th root of
unity in some finite extension field of .
.
The condition that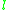 is a quadratic residue
is a quadratic residue
of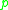 ensures that the coefficients of
ensures that the coefficients of 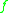
lie in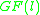 . The dimension of the code is
. The dimension of the code is
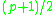
Replacing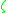 by another primitive
by another primitive 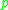 -th
-th
root of unity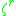 either results in the same code
either results in the same code
or an equivalent code, according to whether or not
is a quadratic residue of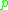 .
.
An alternative construction avoids roots of unity. Define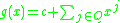
for a suitable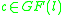 . When
. When 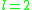
choose to ensure that
to ensure that 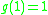
while if is odd
is odd 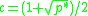
where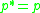 or
or 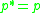 according to whether
according to whether
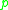 is congruent to
is congruent to 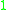 or
or 
modulo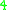 . Then
. Then 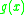 also generates
also generates
a quadratic residue code; more precisely the ideal of
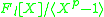 generated by
generated by 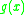
corresponds to the quadratic residue code.
The minimum weight of a quadratic residue code of length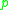
is greater than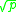 ; this is the square root bound.
; this is the square root bound.
Adding an overall parity-check digit to a quadratic residue code
gives an extended quadratic residue code. When
 (mod
(mod 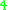 ) an extended quadratic
) an extended quadratic
residue code is self-dual; otherwise it is equivalent but not
equal to its dual. By a theorem of
Gleason and Prange, the automorphism group of an extended quadratic residue
code has a subgroup which is isomorphic to
either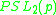 or
or 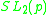 .
.
Examples of quadratic
residue codes include the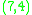 Hamming code
Hamming code
over , the
, the 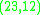 binary Golay code
binary Golay code
over and the
and the 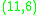 ternary Golay code
ternary Golay code
over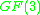 .
.
There is a quadratic residue code of length
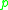
over the finite field
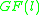 whenever
whenever 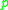
and
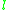 are primes,
are primes,  is odd and
is odd and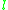 is a quadratic residue modulo
is a quadratic residue modulo 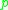 .
.Its generator polynomial as a cyclic code is given by
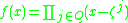
where
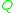 is the set of quadratic residues of
is the set of quadratic residues of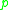 in the set
in the set 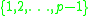 and
and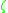 is a primitive
is a primitive 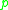 th root of
th root ofunity in some finite extension field of
 .
.The condition that
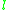 is a quadratic residue
is a quadratic residueof
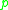 ensures that the coefficients of
ensures that the coefficients of 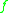
lie in
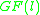 . The dimension of the code is
. The dimension of the code is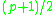
Replacing
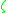 by another primitive
by another primitive 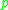 -th
-throot of unity
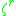 either results in the same code
either results in the same codeor an equivalent code, according to whether or not

is a quadratic residue of
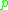 .
.An alternative construction avoids roots of unity. Define
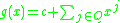
for a suitable
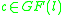 . When
. When 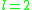
choose
 to ensure that
to ensure that 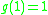
while if
 is odd
is odd 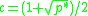
where
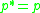 or
or 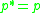 according to whether
according to whether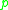 is congruent to
is congruent to 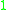 or
or 
modulo
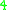 . Then
. Then 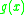 also generates
also generatesa quadratic residue code; more precisely the ideal of
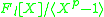 generated by
generated by 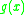
corresponds to the quadratic residue code.
The minimum weight of a quadratic residue code of length
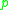
is greater than
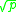 ; this is the square root bound.
; this is the square root bound.Adding an overall parity-check digit to a quadratic residue code
gives an extended quadratic residue code. When
 (mod
(mod 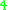 ) an extended quadratic
) an extended quadraticresidue code is self-dual; otherwise it is equivalent but not
equal to its dual. By a theorem of
Gleason and Prange, the automorphism group of an extended quadratic residue
code has a subgroup which is isomorphic to
either
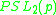 or
or 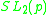 .
.Examples of quadratic
residue codes include the
 Hamming code
Hamming codeHamming code
In telecommunication, Hamming codes are a family of linear error-correcting codes that generalize the Hamming-code invented by Richard Hamming in 1950. Hamming codes can detect up to two and correct up to one bit errors. By contrast, the simple parity code cannot correct errors, and can detect only...
over
 , the
, the  binary Golay code
binary Golay codeBinary Golay code
In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
over
 and the
and the 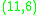 ternary Golay code
ternary Golay codeTernary Golay code
There are two closely related error-correcting codes known as ternary Golay codes. The code generally known simply as the ternary Golay code is a perfect [11, 6, 5] ternary linear code; the extended ternary Golay code is a [12, 6, 6] linear code obtained by adding a zero-sum check digit to the...
over
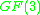 .
.

