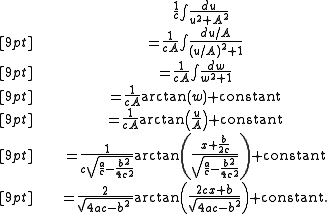Quadratic integral
Encyclopedia
In mathematics
, a quadratic integral is an integral
of the form
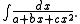
It can be evaluated by completing the square
in the denominator.

q = b2 − 4ac is positive. In that case, define u and A by
 ,
,
and
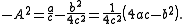
The quadratic integral can now be written as
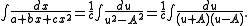
The partial fraction decomposition
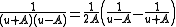
allows us to evaluate the integral:
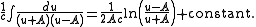
The final result for the original integral, under the assumption that q > 0, is
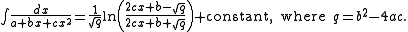
In case the discriminant
q = b2 − 4ac is negative, the second term in the denominator in
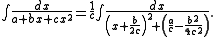
is positive. Then the integral becomes
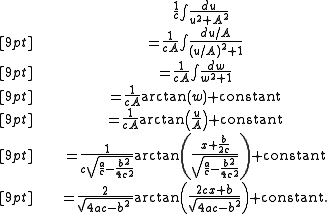
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quadratic integral is an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the form
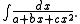
It can be evaluated by completing the square
Completing the square
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the formax^2 + bx + c\,\!to the formIn this context, "constant" means not depending on x. The expression inside the parenthesis is of the form ...
in the denominator.

Positive-discriminant case
Assume that the discriminantDiscriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
q = b2 − 4ac is positive. In that case, define u and A by
 ,
,and
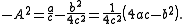
The quadratic integral can now be written as
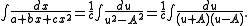
The partial fraction decomposition
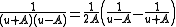
allows us to evaluate the integral:
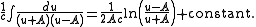
The final result for the original integral, under the assumption that q > 0, is
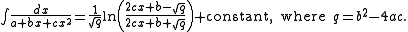
Negative-discriminant case
- This (hastily written) section may need attention.
In case the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
q = b2 − 4ac is negative, the second term in the denominator in
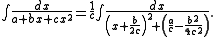
is positive. Then the integral becomes