
Pumping lemma for context-free languages
Encyclopedia
The pumping lemma for context-free languages, also known as the Bar-Hillel
lemma, is a lemma
that gives a property shared by all context-free language
s.
with substrings u, v, x, y and z, such that |vxy| ≤ p, |vy| ≥ 1, and
The property is a property of all strings in the language that are of length at least p, where p is a constant—called the pumping length -- that varies between context-free languages.
Say s is a string of length at least p that is in the language.
The pumping lemma states that s can be split into five substrings,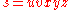 , where vy is non-empty and the length of vxy is at most p, such that repeating v and y any (and the same) number of times in s produces a string that is still in the language (it's possible and often useful to repeat zero times, which removes v and y from the string). This process of "pumping up" additional copies of v and y is what gives the pumping lemma its name.
, where vy is non-empty and the length of vxy is at most p, such that repeating v and y any (and the same) number of times in s produces a string that is still in the language (it's possible and often useful to repeat zero times, which removes v and y from the string). This process of "pumping up" additional copies of v and y is what gives the pumping lemma its name.
Note that finite languages (which are regular and hence context-free) obey the pumping lemma trivially by having p equal to the maximum string length in L plus one. As there are no strings of this length the pumping lemma is not violated.
The pumping lemma is often used to prove that a given language is non-context-free by showing that for each p, we can find some string s of length at least p in the language that does not have the properties outlined above, i.e. that it cannot be "pumped" without producing some strings that are not in the language.
For example, we can show that language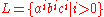 is not context-free by using the pumping lemma in a proof by contradiction. First, assume that
is not context-free by using the pumping lemma in a proof by contradiction. First, assume that  is context free. By the pumping lemma, there exists an integer
is context free. By the pumping lemma, there exists an integer  which is the pumping length of language
which is the pumping length of language 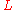 . Consider the string
. Consider the string 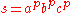 in
in 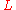 . The pumping lemma tells us that
. The pumping lemma tells us that  can be written in the form
can be written in the form 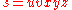 , where
, where 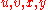 , and
, and  are substrings, such that
are substrings, such that 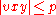 ,
, 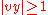 , and
, and 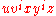 is in
is in 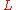 for every integer
for every integer 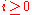 . By our choice of
. By our choice of  and the fact that
and the fact that 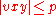 , it is easily seen that the substring
, it is easily seen that the substring 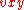 can contain no more than two distinct letters. That is, we have one of five possibilities for
can contain no more than two distinct letters. That is, we have one of five possibilities for 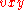 :
:
For each case, it is easily verified that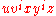 does not contain equal numbers of each letter for any
does not contain equal numbers of each letter for any 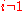 . Thus,
. Thus, 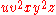 does not have the form
does not have the form 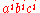 . This contradicts the definition of
. This contradicts the definition of 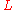 . Therefore, our initial assumption that
. Therefore, our initial assumption that 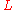 is context free must be false.
is context free must be false.
While the pumping lemma is often a useful tool to prove that a given language is not context-free, it does not give a complete characterization of
the context-free languages. If a language does not satisfy the condition given by the pumping lemma,
we have established that it is not context-free. On the other hand, there are languages that are not context-free, but still
satisfy the condition given by the pumping lemma. There are more powerful proof techniques available, such as Ogden's lemma
, but also these techniques do not give a complete characterization of the context-free languages.
Yehoshua Bar-Hillel
Yehoshua Bar-Hillel was an Israeli philosopher, mathematician, and linguist at the Hebrew University of Jerusalem, best known for his pioneering work in machine translation and formal linguistics.- Biography :...
lemma, is a lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
that gives a property shared by all context-free language
Context-free language
In formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.-Examples:...
s.
Formal statement
If a language L is context-free, then there exists some integer p ≥ 1 such that any string s in L with |s| ≥ p (where p is a pumping length) can be written as- s = uvxyz
with substrings u, v, x, y and z, such that |vxy| ≤ p, |vy| ≥ 1, and
- uv nxy nz is in L for every integer n ≥ 0.
Informal statement and explanation
The pumping lemma for context-free languages (called just "the pumping lemma" from now on) describes a property that all context-free languages are guaranteed to have.The property is a property of all strings in the language that are of length at least p, where p is a constant—called the pumping length -- that varies between context-free languages.
Say s is a string of length at least p that is in the language.
The pumping lemma states that s can be split into five substrings,
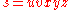 , where vy is non-empty and the length of vxy is at most p, such that repeating v and y any (and the same) number of times in s produces a string that is still in the language (it's possible and often useful to repeat zero times, which removes v and y from the string). This process of "pumping up" additional copies of v and y is what gives the pumping lemma its name.
, where vy is non-empty and the length of vxy is at most p, such that repeating v and y any (and the same) number of times in s produces a string that is still in the language (it's possible and often useful to repeat zero times, which removes v and y from the string). This process of "pumping up" additional copies of v and y is what gives the pumping lemma its name.Note that finite languages (which are regular and hence context-free) obey the pumping lemma trivially by having p equal to the maximum string length in L plus one. As there are no strings of this length the pumping lemma is not violated.
The pumping lemma is often used to prove that a given language is non-context-free by showing that for each p, we can find some string s of length at least p in the language that does not have the properties outlined above, i.e. that it cannot be "pumped" without producing some strings that are not in the language.
Usage of the lemma
The pumping lemma for context-free languages can be used to show that certain languages are not context-free.For example, we can show that language
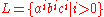 is not context-free by using the pumping lemma in a proof by contradiction. First, assume that
is not context-free by using the pumping lemma in a proof by contradiction. First, assume that 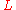 is context free. By the pumping lemma, there exists an integer
is context free. By the pumping lemma, there exists an integer 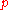 which is the pumping length of language
which is the pumping length of language 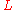 . Consider the string
. Consider the string 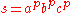 in
in 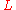 . The pumping lemma tells us that
. The pumping lemma tells us that  can be written in the form
can be written in the form 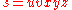 , where
, where 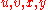 , and
, and  are substrings, such that
are substrings, such that 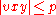 ,
, 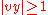 , and
, and 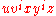 is in
is in  for every integer
for every integer 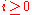 . By our choice of
. By our choice of  and the fact that
and the fact that 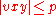 , it is easily seen that the substring
, it is easily seen that the substring 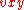 can contain no more than two distinct letters. That is, we have one of five possibilities for
can contain no more than two distinct letters. That is, we have one of five possibilities for 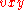 :
:
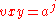 for some
for some 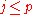 .
.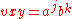 for some
for some 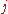 and
and 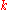 with
with 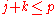 .
.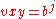 for some
for some 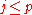 .
.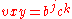 for some
for some 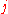 and
and 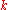 with
with 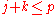 .
.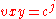 for some
for some 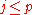 .
.
For each case, it is easily verified that
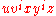 does not contain equal numbers of each letter for any
does not contain equal numbers of each letter for any 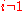 . Thus,
. Thus, 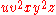 does not have the form
does not have the form 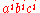 . This contradicts the definition of
. This contradicts the definition of 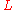 . Therefore, our initial assumption that
. Therefore, our initial assumption that 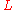 is context free must be false.
is context free must be false.While the pumping lemma is often a useful tool to prove that a given language is not context-free, it does not give a complete characterization of
the context-free languages. If a language does not satisfy the condition given by the pumping lemma,
we have established that it is not context-free. On the other hand, there are languages that are not context-free, but still
satisfy the condition given by the pumping lemma. There are more powerful proof techniques available, such as Ogden's lemma
Ogden's lemma
In the theory of formal languages, Ogden's lemma provides an extension of flexibility over the pumping lemma for context-free languages....
, but also these techniques do not give a complete characterization of the context-free languages.

