Basic definitions

LU is the set of all lower bounds of the set of all upper bound

Upper bound

In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...

s of the subset A of a partially ordered set

Partially ordered set

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

.

A subset I of a partially ordered set (P,≤) is a Doyle pseudoideal, if the following condition holds:

For every finite subset S of P which has a supremum

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

 in P, S 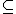I implies that LU(S) I.

A subset I of a partially ordered set (P,≤) is a pseudoideal, if the following condition holds:

For every subset S of P having at most two elements which has a supremum

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

 in P, S 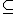I implies that LU(S) I.

Remarks

1. Every Frink ideal
   Frink ideal
   In mathematics, a Frink ideal, introduced by Orrin Frink, is a certain kind of subset of a partially ordered set.- Basic definitions :LU is the set of all lower bounds of the set of all upper bounds of the subset A of a partially ordered set....
   
    I is a Doyle pseudoideal.
2. A subset I of a lattice (P,≤) is a Doyle pseudoideal if and only if
   If and only if
   In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
   
    it is a lower set that is closed under finite joins (suprema).