
Pseudo-Boolean function
Encyclopedia
In mathematics
and optimization
, a pseudo-Boolean function is a function
of the form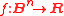 ,
,
where B = {0, 1} is a Boolean domain
and n is a nonnegative integer called the arity
of the function. Any pseudo-Boolean function can be written uniquely as a multi-linear polynomial:
An important class of pseudo-Boolean functions are the submodular functions, because polynomimal-time algorithms exists for minimizing them. The degree of the pseudo-Boolean function is simply the degree of the polynomial.
In many settings (e.g., in Fourier analysis of pseudo-Boolean functions), a pseudo-Boolean function is viewed as a function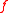 that maps
that maps 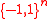 to
to  . Again in this case we can uniquely write
. Again in this case we can uniquely write 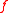 as a multi-linear polynomial:
as a multi-linear polynomial:
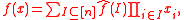 where
where 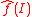 are Fourier coefficients of
are Fourier coefficients of  and
and 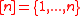 . For a nice and simple introduction to Fourier analysis of pseudo-Boolean functions, see .
. For a nice and simple introduction to Fourier analysis of pseudo-Boolean functions, see .
. This can easily be seen by formulating, for example, the maximum cut
problem as maximizing a pseudo-Boolean function.
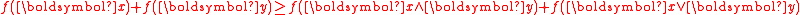
for every x and y. This is a very importand concept, because a submodular pseudo-boolean function can be minimized in polynomial time.
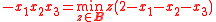
There are other possibilities, for example,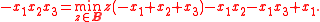
Different reductions lead to different results. Take for example the following cubic polynomial: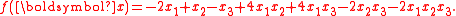
Using the first reduction followed by roof duality, we obtain a lower bound of -3 and no indication on how to assign the three variables. Using the second reduction, we obtain the (tight) lower bound of -2 and the optimal assignment of every variable (which is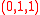 ).
).
 as a mapping from
as a mapping from 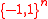 to
to  . Then
. Then 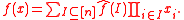 Assume that each coefficient
Assume that each coefficient 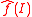 is integral.
is integral.
Then for an integer the problem P of deciding whether
the problem P of deciding whether 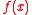 is more or equal to
is more or equal to  is NP-complete. It is proved in that
is NP-complete. It is proved in that
in polynomial time we can either solve P or reduce the number of variables to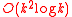 .
.
Let be the degree of the above multi-linear polynomial for
be the degree of the above multi-linear polynomial for 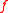 . Then proved that in polynomial time we can either solve P or reduce the number of variables to
. Then proved that in polynomial time we can either solve P or reduce the number of variables to 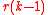 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and optimization
Optimization
Optimization or optimality may refer to:* Mathematical optimization, the theory and computation of extrema or stationary points of functionsEconomics and business* Optimality, in economics; see utility and economic efficiency...
, a pseudo-Boolean function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the form
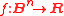 ,
,where B = {0, 1} is a Boolean domain
Boolean domain
In mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true...
and n is a nonnegative integer called the arity
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
of the function. Any pseudo-Boolean function can be written uniquely as a multi-linear polynomial:

An important class of pseudo-Boolean functions are the submodular functions, because polynomimal-time algorithms exists for minimizing them. The degree of the pseudo-Boolean function is simply the degree of the polynomial.
In many settings (e.g., in Fourier analysis of pseudo-Boolean functions), a pseudo-Boolean function is viewed as a function
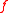 that maps
that maps 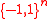 to
to  . Again in this case we can uniquely write
. Again in this case we can uniquely write 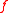 as a multi-linear polynomial:
as a multi-linear polynomial: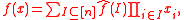 where
where 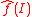 are Fourier coefficients of
are Fourier coefficients of  and
and 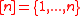 . For a nice and simple introduction to Fourier analysis of pseudo-Boolean functions, see .
. For a nice and simple introduction to Fourier analysis of pseudo-Boolean functions, see .Optimization
Minimizing (or, equivalently, maximizing) a pseudo-Boolean function is NP-HardNP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
. This can easily be seen by formulating, for example, the maximum cut
Maximum cut
For a graph, a maximum cut is a cut whose size is at least the size of any other cut. The problem of finding a maximum cut in a graph is known as the max-cut problem.The problem can be stated simply as follows...
problem as maximizing a pseudo-Boolean function.
Submodularity
A pseudo-Boolean function f is said to be submodular if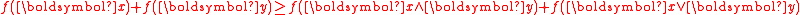
for every x and y. This is a very importand concept, because a submodular pseudo-boolean function can be minimized in polynomial time.
Roof Duality
If f is a quadratic polynomial, a concept called roof duality can be used to obtain a lower bound for its minimum value. Roof duality may also provide a partial assignment of the variables, indicating some of the values of a minimizer to the polynomial. Several different methods of obtaining lower bounds were developed only to later be shown to be equivalent to what is now called roof duality.Reductions
If the degree of f is greater than 2, one can always employ reductions to obtain an equivalent quadratic problem with additional variables. One possible reduction is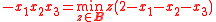
There are other possibilities, for example,
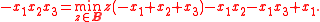
Different reductions lead to different results. Take for example the following cubic polynomial:
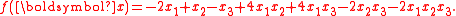
Using the first reduction followed by roof duality, we obtain a lower bound of -3 and no indication on how to assign the three variables. Using the second reduction, we obtain the (tight) lower bound of -2 and the optimal assignment of every variable (which is
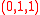 ).
).Polynomial Compression Algorithms
Consider a pseudo-Boolean function as a mapping from
as a mapping from 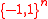 to
to  . Then
. Then 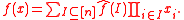 Assume that each coefficient
Assume that each coefficient 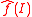 is integral.
is integral.Then for an integer
 the problem P of deciding whether
the problem P of deciding whether 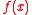 is more or equal to
is more or equal to  is NP-complete. It is proved in that
is NP-complete. It is proved in thatin polynomial time we can either solve P or reduce the number of variables to
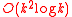 .
.Let
 be the degree of the above multi-linear polynomial for
be the degree of the above multi-linear polynomial for 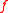 . Then proved that in polynomial time we can either solve P or reduce the number of variables to
. Then proved that in polynomial time we can either solve P or reduce the number of variables to 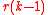 .
.

