
Prouhet-Tarry-Escott problem
Encyclopedia
In mathematics, the Prouhet–Tarry–Escott problem asks for two disjoint sets A and B of n integer
s each, such that:
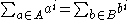
for each integer i from 1 to a given k.
This problem was named after Eugène Prouhet, who studied it in the early 1850s, and Gaston Tarry
and Escott, who studied it in the early 1910s.
The largest value of k for which a solution with n = k+1 is known is given by A = {±22, ±61, ±86, ±127, ±140, ±151}, B = {±35, ±47, ±94, ±121, ±146, ±148} for which k = 11.
and { 1, 2, 10, 12, 20, 21 }, because:
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s each, such that:
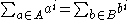
for each integer i from 1 to a given k.
This problem was named after Eugène Prouhet, who studied it in the early 1850s, and Gaston Tarry
Gaston Tarry
Gaston Tarry was a French mathematician. Born in Villefranche de Rouergue, Aveyron, he studied mathematics at high school before joining the civil service in Algeria....
and Escott, who studied it in the early 1910s.
The largest value of k for which a solution with n = k+1 is known is given by A = {±22, ±61, ±86, ±127, ±140, ±151}, B = {±35, ±47, ±94, ±121, ±146, ±148} for which k = 11.
Example
For example, a solution with n = 6 and k = 5 is the two sets { 0, 5, 6, 16, 17, 22 }and { 1, 2, 10, 12, 20, 21 }, because:
- 01 + 51 + 61 + 161 + 171 + 221 = 11 + 21 + 101 + 121 + 201 + 211
- 02 + 52 + 62 + 162 + 172 + 222 = 12 + 22 + 102 + 122 + 202 + 212
- 03 + 53 + 63 + 163 + 173 + 223 = 13 + 23 + 103 + 123 + 203 + 213
- 04 + 54 + 64 + 164 + 174 + 224 = 14 + 24 + 104 + 124 + 204 + 214
- 05 + 55 + 65 + 165 + 175 + 225 = 15 + 25 + 105 + 125 + 205 + 215.
See also
- Thue–Morse sequence
- Euler's sum of powers conjecture

