
Product numerical range
Encyclopedia
Given a Hilbert space
with a tensor product
structure a product numerical range is defined as a numerical range
with respect to the subset of product vectors. In some situations, especially in the context of quantum mechanics
product numerical range is known as local numerical range
Introduction =
Let be an operator acting on an
be an operator acting on an  -dimensional Hilbert space
-dimensional Hilbert space  . Let
. Let 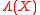 denote its numerical range, i.e. the set of all
denote its numerical range, i.e. the set of all  such that there exists a normalized state
such that there exists a normalized state  ,
,  , which satisfies
, which satisfies 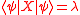 .
.
An analogous notion can be defined for operators acting on a composite Hilbert space with a tensor product structure. Consider first a bi–partite Hilbert space, of a composite dimension
of a composite dimension  .
.
 be an operator acting on the composite Hilbert space. We define the product numerical range
be an operator acting on the composite Hilbert space. We define the product numerical range 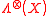 of
of  , with respect to the tensor product structure of
, with respect to the tensor product structure of  , as
, as 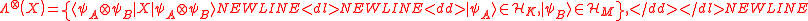 where
where 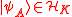 and
and  are normalized.
are normalized.
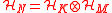 be a tensor product Hilbert space. We define the product numerical radius
be a tensor product Hilbert space. We define the product numerical radius  of
of  , with respect to this tensor product structure, as
, with respect to this tensor product structure, as 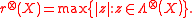
The product numerical range can be considered as a particular case of the decomposable numerical range defined for operators acting on a tensor product Hilbert space. This notion may also be considered as a numerical range relative to the proper subgroup of the full unitary group
of the full unitary group 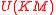 .
.
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
with a tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
structure a product numerical range is defined as a numerical range
Numerical range
In the mathematical field of linear algebra and convex analysis, the numerical range of a square matrix with complex entries is a subset of the complex plane associated to the matrix...
with respect to the subset of product vectors. In some situations, especially in the context of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
product numerical range is known as local numerical range
Introduction =
Let
 be an operator acting on an
be an operator acting on an  -dimensional Hilbert space
-dimensional Hilbert space  . Let
. Let 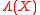 denote its numerical range, i.e. the set of all
denote its numerical range, i.e. the set of all  such that there exists a normalized state
such that there exists a normalized state  ,
,  , which satisfies
, which satisfies 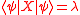 .
.An analogous notion can be defined for operators acting on a composite Hilbert space with a tensor product structure. Consider first a bi–partite Hilbert space,
 of a composite dimension
of a composite dimension  .
.Product numerical range
Let be an operator acting on the composite Hilbert space. We define the product numerical range
be an operator acting on the composite Hilbert space. We define the product numerical range 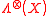 of
of  , with respect to the tensor product structure of
, with respect to the tensor product structure of  , as
, as 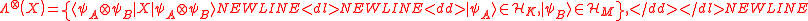 where
where 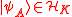 and
and  are normalized.
are normalized.Product numerical radius
Let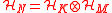 be a tensor product Hilbert space. We define the product numerical radius
be a tensor product Hilbert space. We define the product numerical radius  of
of  , with respect to this tensor product structure, as
, with respect to this tensor product structure, as 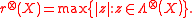
Notation
The notion of numerical range of a given operator, also called “field of values”, has been extensively studied during the last few decades and its usefulness in quantum theory has been emphasized. Several generalizations of numerical range are known. In particular, Marcus introduced the notion of ’’’decomposable numerical range’’’, the properties of which are a subject of considerable interest.The product numerical range can be considered as a particular case of the decomposable numerical range defined for operators acting on a tensor product Hilbert space. This notion may also be considered as a numerical range relative to the proper subgroup
 of the full unitary group
of the full unitary group 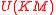 .
.General case
It is not difficult to establish the basic properties of the product numerical range which are independent of the partition of the Hilbert space and of the structure of the operator. We list them below leaving some simple items without a proof.Basic properties
Topological facts concerning product numerical range for general operators.- Product numerical range forms a connected set in the complex plane. This is true because product numerical range is a continuous image of a connected set.
- Product numerical range is subadditive. For all
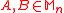
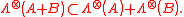
- For all
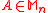 and
and 

- For all
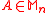 and
and 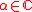

- For all

 for unitary
for unitary  and
and  .
. - Let
 and
and 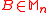
- If one of them is normal then the numerical range of their tensor product coincides with the convex hull of the product numerical range,

- If
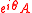 is positive semidefinite for some
is positive semidefinite for some 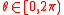 , then
, then 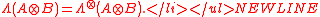
- Let
 and
and 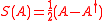 .
.
- For all
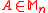 , we have
, we have  and
and 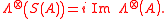
Convexity
The product numerical range does not need to be convex. Consider the following simple example. Let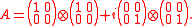
Matrix defined above is matrix with eigenvalues
defined above is matrix with eigenvalues 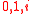 . It is easy to see that
. It is easy to see that 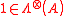 and
and 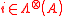 , but
, but  . Actually, by direct computation we have
. Actually, by direct computation we have 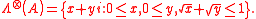
Product numerical range of matrix is presented below.
is presented below.
Product numerical range forms a nonempty set for a general operator. In particular it contains the barycenter of the spectrum.
Barycenter
Product numerical range of includes the barycenter of the spectrum,
includes the barycenter of the spectrum, 
Product numerical radius is a vector norm on matrices, but it is not a matrix norm. Product numerical radius is invariant with respect to local unitaries, which have the tensor product structure.
- Let
- If
- If one of them is normal then the numerical range of their tensor product coincides with the convex hull of the product numerical range,

