The Prandtl–Glauert singularity is the prediction by the Prandtl–Glauert transformation

Prandtl–Glauert transformation

The Prandtl–Glauert transformation or Prandtl–Glauert rule is an approximation function which allows comparison of aerodynamical processes occurring at different Mach numbers.- Mathematical expression :...

 that infinite pressure conditions would be experienced by an aircraft as it approaches the speed of sound

Speed of sound

The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....

. Because it is invalid to apply the transformation at these speeds, the predicted singularity does not emerge. This is related to the early 20th century misconception of the impenetrability of the sound barrier

Sound barrier

The sound barrier, in aerodynamics, is the point at which an aircraft moves from transonic to supersonic speed. The term, which occasionally has other meanings, came into use during World War II, when a number of aircraft started to encounter the effects of compressibility, a collection of several...

.

Prandtl-Glauert Transformation

The Prandtl-Glauert transformation is found by linearizing the potential equations associated with compressible, inviscid flow. It was discovered that the linearized pressures in such a flow were equal to those found from incompressible flow theory multiplied by a correction factor. This correction factor is given below: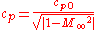

where

• c_p is the compressible pressure coefficient
  Pressure coefficient
  The pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field in fluid dynamics. The pressure coefficient is used in aerodynamics and hydrodynamics...
  
  
• c_p0 is the incompressible pressure coefficient
  Pressure coefficient
  The pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field in fluid dynamics. The pressure coefficient is used in aerodynamics and hydrodynamics...
  
  
• M_∞ is the freestream Mach number.

This correction factor works well up to low-transonic Mach numbers (M < ~0.7). However, note the limit:



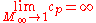
This obviously nonphysical result (of an infinite pressure) is known as the Prandtl-Glauert singularity.