
Population stratification
Encyclopedia
Population stratification is the presence of a systematic difference in allele
frequencies
between subpopulations in a population
possibly due to different ancestry
, especially in the context of association studies. Population stratification is also referred to as population structure, in this context.
be controlled for using methods such as the TDT
. But if the structure is known or a putative structure is found, there are a
number of possible ways to implement this structure in the association studies and thus
compensate for any population bias. Most contemporary
genome-wide association studies take the view that the problem of population stratification is
manageable , and that the logistic advantages of using unrelated cases and controls make these
studies preferable to family-based association studies.
The two most widely used approaches to this problem include genomic control, which is a relatively nonparametric method for controlling the inflation of test statistics , and structured association methods , which use genetic information to estimate and control for population structure. Currently, the most widely used structured association method is Eigenstrat, developed by Alkes Price and colleagues .
studies, can easily be violated and can lead to both type I and type II errors
. It is
therefore important for the models used in the study to compensate for the population
structure. The problem in case control studies is that if there is a genetic involvement in
the disease, the case population is more likely to be related than the individuals in the
control population. This means that the assumption of independence of observations is
violated. Often this will lead to an overestimation of the significance of an association
but it depends on the way the sample was chosen. As long as there is a higher allele
frequency in a subpopulation you will find association with any trait more prevalent
in the case population . This kind of spurious association
increases as the sample population grows so the problem should be of special concern in
large scale association studies when loci only cause relatively small effects on the trait. A method that in some cases can compensate for the above described problems has been developed by Devlin and
Roeder (1999). It uses both a frequentist and a Bayesian approach (the latter being
appropriate when dealing with a large number of candidate genes). Here is a short description of how the frequentist way of correcting for population stratification works. It works by using markers that are not linked with the trait in question to correct
for any inflation of the statistic caused by population stratification. The method was
first developed for binary traits but has since been generalized for quantitative ones
. For the binary one, which applies to finding genetic differences
between the case and control populations, Devlin and Roeder (1999) use Armitage’s
trend test
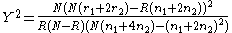
and the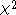 test for allelic frequencies
test for allelic frequencies
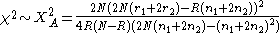
If the population is in Hardy-Weinberg equilibrium the two statistics are approximately
equal. Under the null hypothesis of no population stratification the trend test is
asymptotic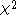 distribution with one degree of freedom.
distribution with one degree of freedom.
The idea is that the statistic is inflated by a factor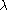 so that
so that 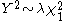 where
where  depends on the effect of stratification. The above method rests upon the assumption that the inflation
depends on the effect of stratification. The above method rests upon the assumption that the inflation
factor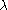 is constant, which means that the loci should have roughly equal mutation
is constant, which means that the loci should have roughly equal mutation
rates, should not be under different selection in the two populations, and the amount of
Hardy-Weinberg disequilibrium measured in Wright’s coefficient of inbreeding F should
not differ between the different loci. The latter being of greatest concern. If the effect of
the stratification is similar across the different loci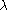 can be estimated from the unlinked
can be estimated from the unlinked
markers
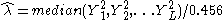
where L is the number of unlinked markers. The denominator
is derived from the gamma distribution as a robust estimator of . Other estimators
. Other estimators
have been suggested, for example, suggested using the mean
of the statistics instead.
This is not the only way to estimate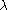 but according to it is an
but according to it is an
appropriate estimate even if some of the unlinked markers are actually in disequilibrium
with a disease causing locus or are themselves associated with the disease. Under the
null hypothesis and when correcting for stratification using L unlinked genes,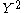 is
is
approximately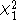
distributed. With this correction the
overall type I error rate should be approximately equal to even when the population
even when the population
is stratified.
Devlin and Roeder (1999) mostly considered the situation where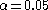 gives a
gives a
95% confidence level and not smaller p-values. Marchini et al. (2004) demonstrates by
simulation that genomic control can lead to an anti-conservative p-value if this value
is very small and the two populations (case and control) are extremely distinct. This
was especially a problem if the number of unlinked markers were in the order 50 − 100.
This can result in false positives (at that significance level).
Allele
An allele is one of two or more forms of a gene or a genetic locus . "Allel" is an abbreviation of allelomorph. Sometimes, different alleles can result in different observable phenotypic traits, such as different pigmentation...
frequencies
Allele frequency
Allele frequency or Gene frequency is the proportion of all copies of a gene that is made up of a particular gene variant . In other words, it is the number of copies of a particular allele divided by the number of copies of all alleles at the genetic place in a population. It can be expressed for...
between subpopulations in a population
Population
A population is all the organisms that both belong to the same group or species and live in the same geographical area. The area that is used to define a sexual population is such that inter-breeding is possible between any pair within the area and more probable than cross-breeding with individuals...
possibly due to different ancestry
Ancestor
An ancestor is a parent or the parent of an ancestor ....
, especially in the context of association studies. Population stratification is also referred to as population structure, in this context.
Causes of population stratification
The basic cause of population stratification is nonrandom mating between groups, often due to their physical separation (e.g., for populations of African and European descent) followed by genetic drift of allele frequencies in each group. In some contemporary populations there has been recent admixture between individuals from different populations, leading to populations in which ancestry is variable (as in African Americans). Over tens of generations, random mating can eliminate this type of stratification. In some parts of the globe (e.g., in Europe), population structure is best modeled by isolation-by-distance, in which allele frequencies tend to vary smoothly with location.Population stratification and association studies
Population stratification can be a problem for association studies, such as case-control studies, where the association found could be due to the underlying structure of the population and not a disease associated locus. Also the real disease causing locus might not be found in the study if the locus is less prevalent in the population where the case subjects are chosen. For this reason, it was common in the 1990s to use family-based data where the effect of population stratification can easilybe controlled for using methods such as the TDT
Transmission disequilibrium test
The transmission disequilibrium test was proposed by Spielman, McGinnis and Ewens as a family-based association test for the presence of genetic linkage between a genetic marker and a trait...
. But if the structure is known or a putative structure is found, there are a
number of possible ways to implement this structure in the association studies and thus
compensate for any population bias. Most contemporary
genome-wide association studies take the view that the problem of population stratification is
manageable , and that the logistic advantages of using unrelated cases and controls make these
studies preferable to family-based association studies.
The two most widely used approaches to this problem include genomic control, which is a relatively nonparametric method for controlling the inflation of test statistics , and structured association methods , which use genetic information to estimate and control for population structure. Currently, the most widely used structured association method is Eigenstrat, developed by Alkes Price and colleagues .
Genomic Control
The assumption of population homogeneity in association studies, especially case-controlstudies, can easily be violated and can lead to both type I and type II errors
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
. It is
therefore important for the models used in the study to compensate for the population
structure. The problem in case control studies is that if there is a genetic involvement in
the disease, the case population is more likely to be related than the individuals in the
control population. This means that the assumption of independence of observations is
violated. Often this will lead to an overestimation of the significance of an association
but it depends on the way the sample was chosen. As long as there is a higher allele
frequency in a subpopulation you will find association with any trait more prevalent
in the case population . This kind of spurious association
increases as the sample population grows so the problem should be of special concern in
large scale association studies when loci only cause relatively small effects on the trait. A method that in some cases can compensate for the above described problems has been developed by Devlin and
Roeder (1999). It uses both a frequentist and a Bayesian approach (the latter being
appropriate when dealing with a large number of candidate genes). Here is a short description of how the frequentist way of correcting for population stratification works. It works by using markers that are not linked with the trait in question to correct
for any inflation of the statistic caused by population stratification. The method was
first developed for binary traits but has since been generalized for quantitative ones
. For the binary one, which applies to finding genetic differences
between the case and control populations, Devlin and Roeder (1999) use Armitage’s
trend test
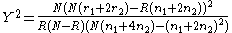
and the
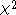 test for allelic frequencies
test for allelic frequencies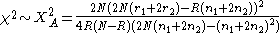
| Alleles | aa | Aa | AA | total |
|---|---|---|---|---|
| Case | r0 | r1 | r2 | R |
| Control | s0 | s1 | s2 | S |
| total | n0 | n1 | n2 | N |
If the population is in Hardy-Weinberg equilibrium the two statistics are approximately
equal. Under the null hypothesis of no population stratification the trend test is
asymptotic
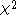 distribution with one degree of freedom.
distribution with one degree of freedom.The idea is that the statistic is inflated by a factor
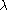 so that
so that 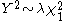 where
where  depends on the effect of stratification. The above method rests upon the assumption that the inflation
depends on the effect of stratification. The above method rests upon the assumption that the inflationfactor
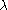 is constant, which means that the loci should have roughly equal mutation
is constant, which means that the loci should have roughly equal mutationrates, should not be under different selection in the two populations, and the amount of
Hardy-Weinberg disequilibrium measured in Wright’s coefficient of inbreeding F should
not differ between the different loci. The latter being of greatest concern. If the effect of
the stratification is similar across the different loci
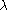 can be estimated from the unlinked
can be estimated from the unlinkedmarkers
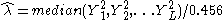
where L is the number of unlinked markers. The denominator
is derived from the gamma distribution as a robust estimator of
 . Other estimators
. Other estimatorshave been suggested, for example, suggested using the mean
of the statistics instead.
This is not the only way to estimate
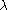 but according to it is an
but according to it is anappropriate estimate even if some of the unlinked markers are actually in disequilibrium
with a disease causing locus or are themselves associated with the disease. Under the
null hypothesis and when correcting for stratification using L unlinked genes,
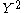 is
isapproximately
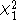
distributed. With this correction the
overall type I error rate should be approximately equal to
 even when the population
even when the populationis stratified.
Devlin and Roeder (1999) mostly considered the situation where
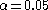 gives a
gives a95% confidence level and not smaller p-values. Marchini et al. (2004) demonstrates by
simulation that genomic control can lead to an anti-conservative p-value if this value
is very small and the two populations (case and control) are extremely distinct. This
was especially a problem if the number of unlinked markers were in the order 50 − 100.
This can result in false positives (at that significance level).

