
Polynomial chaos
Encyclopedia
Polynomial chaos , also called "Wiener Chaos expansion", is a non-sampling based method to determine evolution of uncertainty in dynamical system, when there is probabilistic uncertainty in the system parameters.
PC was first introduced by Wiener where Hermite polynomials were used to model stochastic processes with Gaussian random variables. It can be thought of as an extension of Volterra's theory of nonlinear
functionals for stochastic systems. According to Cameron and Martin such an expansion converges in the
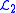 sense for any arbitrary stochastic process with
sense for any arbitrary stochastic process with
finite second moment. This applies to most physical systems. Xiu generalized the result of Cameron-Martin to various
continuous and discrete distributions using orthogonal polynomials
from the so called Askey-scheme and
demonstrated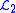 convergence in the corresponding Hilbert
convergence in the corresponding Hilbert
functional space. This is popularly known as the generalized
polynomial chaos (gPC) framework. The gPC framework has been applied to applications including
stochastic fluid dynamics, stochastic finite elements, solid mechanics, nonlinear estimation, and probabilistic robust control. It has been demonstrated that gPC based methods are computationally superior to Monte-Carlo based methods in a number of applications. However, the method has a notable limitation. For large numbers of random variables, polynomial chaos becomes very computationally expensive and Monte-Carlo methods are typically more feasible.
PC was first introduced by Wiener where Hermite polynomials were used to model stochastic processes with Gaussian random variables. It can be thought of as an extension of Volterra's theory of nonlinear
functionals for stochastic systems. According to Cameron and Martin such an expansion converges in the
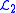 sense for any arbitrary stochastic process with
sense for any arbitrary stochastic process withfinite second moment. This applies to most physical systems. Xiu generalized the result of Cameron-Martin to various
continuous and discrete distributions using orthogonal polynomials
from the so called Askey-scheme and
demonstrated
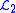 convergence in the corresponding Hilbert
convergence in the corresponding Hilbertfunctional space. This is popularly known as the generalized
polynomial chaos (gPC) framework. The gPC framework has been applied to applications including
stochastic fluid dynamics, stochastic finite elements, solid mechanics, nonlinear estimation, and probabilistic robust control. It has been demonstrated that gPC based methods are computationally superior to Monte-Carlo based methods in a number of applications. However, the method has a notable limitation. For large numbers of random variables, polynomial chaos becomes very computationally expensive and Monte-Carlo methods are typically more feasible.

