Polar set (potential theory)
Encyclopedia
In mathematics
, in the area of classical potential theory
, polar sets are the "negligible sets", similar to the way in which sets of measure zero are the negligible set
s in measure theory.
in 
(where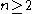 
) is a polar set if there is a non-constant subharmonic function
on 
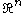
such that
Note that there are other (equivalent) ways in which polar sets may be defined, such as by replacing "subharmonic" by "superharmonic", and
by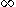 
in the definition above.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of classical potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
, polar sets are the "negligible sets", similar to the way in which sets of measure zero are the negligible set
Negligible set
In mathematics, a negligible set is a set that is small enough that it can be ignored for some purpose.As common examples, finite sets can be ignored when studying the limit of a sequence, and null sets can be ignored when studying the integral of a measurable function.Negligible sets define...
s in measure theory.
Definition
A set in (where 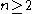) is a polar set if there is a non-constant subharmonic functionSubharmonic function
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
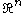
on such that
Note that there are other (equivalent) ways in which polar sets may be defined, such as by replacing "subharmonic" by "superharmonic", and
by 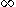in the definition above.Properties
The most important properties of polar sets are:- A singleton set in
is polar. - A countable set in
is polar. - The union of a countable collection of polar sets is polar.
- A polar set has Lebesgue measure zero in
