Poinsot's construction
Encyclopedia
In classical mechanics
, Poinsot's construction is a geometrical method for visualizing the torque-free motion of a rotating rigid body
, that is, the motion of a rigid body on which no external forces are acting. This motion has four constants: the kinetic energy
of the body and the three components of the angular momentum
, expressed with respect to an inertial laboratory frame. The angular velocity
vector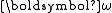
of the rigid rotor
is not constant, but satisfies Euler's equations. Without explicitly solving these equations, Louis Poinsot
was able to visualize the motion of the endpoint of the angular velocity vector. To this end he used the conservation of kinetic energy and angular momentum as constraints on the motion of the angular velocity vector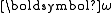
. If the rigid rotor is symmetric (has two equal moments of inertia), the vector 
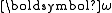describes a cone (and its endpoint a circle). This is the torque-free precession
of the rotation axis of the rotor.
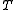is conserved so 
.
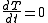The angular kinetic energy may be expressed in terms of the moment of inertia tensor
and the angular velocity vector 
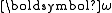
where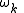
are the components of the angular velocity
vector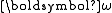
along the principal axes, and the 
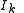are the principal moments of inertia
. Thus, the conservation of kinetic energy imposes a constraint on the three-dimensional angular velocity
vector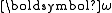
; in the principal axis frame, it must lie on an ellipsoid, called inertia ellipsoid.
The ellipsoid axes values are the half of the principal moments of inertia. The path traced out on this ellipsoid by the angular velocity vector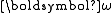
is called the polhode
(coined by Poinsot from Greek roots for "pole path") and is generally circular or taco
-shaped.
is conserved in an inertial reference frame
.
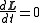The angular momentum vector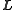
can be expressed
in terms of the moment of inertia tensor
and the angular velocity vector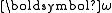 
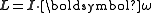
which leads to the equation
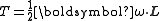
Since the dot product of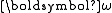
and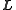 
is constant, and 
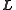itself is constant, the angular velocity vector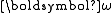 
has a constant component in the direction of the angular momentum vector
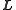. This imposes a second constraint on the vector 
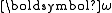; in absolute space, it must lie on an
invariable plane defined by its dot product with the conserved vector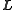
. The normal vector to the invariable plane is aligned with 
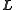. The path traced out by the angular velocity vector 
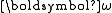on the invariable plane is called the herpolhode (coined from Greek roots for "serpentine pole path"). The etymology of "herpolhode" is obscure, since most herpolhodes are simple circles, not sinusoidal; Poinsot may have been thinking of the ouroboros
, the symbol of endless cycling.
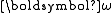equals the angular momentum vector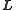 
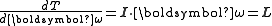
Hence, the normal vector to the kinetic-energy ellipsoid at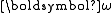
is
proportional to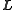
, which is also true of the invariable plane.
Since their normal vectors point in the same direction, these two surfaces will intersect tangentially.
Taken together, these results show that, in an absolute reference frame, the instantaneous angular velocity vector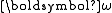
is the point of intersection between a fixed invariable plane and a kinetic-energy ellipsoid that is tangent to it and rolls around on it without slipping. This is Poinsot's construction.
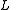of the angular momentum and the kinetic energy 
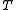are both conserved
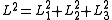
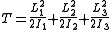
where the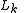
are the components of the angular momentum vector along the principal axes, and the 
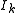are the principal moments of inertia.
These conservation laws are equivalent to two constraints to the three-dimensional angular momentum vector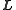
.
The kinetic energy constrains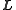
to lie on an
ellipsoid, whereas the angular momentum constraint constrains
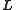to lie on a sphere
. These two surfaces
intersect in taco-shaped curves that define the possible solutions
for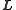
.
This construction differs from Poinsot's construction because it considers
the angular momentum vector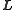
rather than the angular velocity vector 
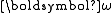. It appears to have been developed by Jacques Philippe Marie Binet
.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, Poinsot's construction is a geometrical method for visualizing the torque-free motion of a rotating rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
, that is, the motion of a rigid body on which no external forces are acting. This motion has four constants: the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the body and the three components of the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, expressed with respect to an inertial laboratory frame. The angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector
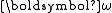of the rigid rotorRigid rotor
The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
is not constant, but satisfies Euler's equations. Without explicitly solving these equations, Louis Poinsot
Louis Poinsot
Louis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...
was able to visualize the motion of the endpoint of the angular velocity vector. To this end he used the conservation of kinetic energy and angular momentum as constraints on the motion of the angular velocity vector
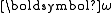. If the rigid rotor is symmetric (has two equal moments of inertia), the vector 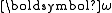describes a cone (and its endpoint a circle). This is the torque-free precessionPrecession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of the rotation axis of the rotor.
Angular kinetic energy constraint
In the absence of applied torques, the angular kinetic energy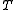 is conserved so 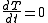.The angular kinetic energy may be expressed in terms of the moment of inertia tensor
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
and the angular velocity vector 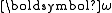where
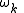are the components of the angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector
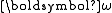along the principal axes, and the 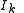are the principal moments of inertiaMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
. Thus, the conservation of kinetic energy imposes a constraint on the three-dimensional angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector
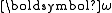; in the principal axis frame, it must lie on an ellipsoid, called inertia ellipsoid.The ellipsoid axes values are the half of the principal moments of inertia. The path traced out on this ellipsoid by the angular velocity vector
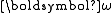is called the polhodePolhode
The details of a spinning body may impose restrictions on the motion of its angular velocity vector, ω. The curve produced by the angular velocity vector on the inertia ellipsoid, is known as the polhode, coined from Greek meaning "path of the pole"...
(coined by Poinsot from Greek roots for "pole path") and is generally circular or taco
Taco
A taco is a traditional Mexican dish composed of a corn or wheat tortilla folded or rolled around a filling. A taco can be made with a variety of fillings, including beef, chicken, seafood, vegetables and cheese, allowing for great versatility and variety...
-shaped.
Angular momentum constraint
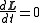In the absence of applied torques, the angular momentum vector is conserved in an inertial reference frame.The angular momentum vector
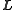can be expressedin terms of the moment of inertia tensor
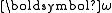
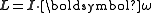
and the angular velocity vector which leads to the equation
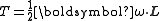
Since the dot product of
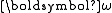and 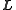is constant, and 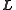itself is constant, the angular velocity vector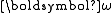 has a constant component in the direction of the angular momentum vector
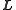. This imposes a second constraint on the vector 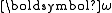; in absolute space, it must lie on aninvariable plane defined by its dot product with the conserved vector
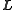. The normal vector to the invariable plane is aligned with 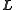. The path traced out by the angular velocity vector 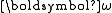on the invariable plane is called the herpolhode (coined from Greek roots for "serpentine pole path"). The etymology of "herpolhode" is obscure, since most herpolhodes are simple circles, not sinusoidal; Poinsot may have been thinking of the ouroborosOuroboros
The Ouroboros is an ancient symbol depicting a serpent or dragon eating its own tail. The name originates from within Greek language; οὐρά meaning "tail" and βόρος meaning "eating", thus "he who eats the tail"....
, the symbol of endless cycling.
Tangency condition and construction
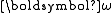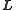
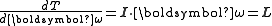
These two constraints operate in different reference frames; the ellipsoidal constraint holds in the (rotating) principal axis frame, whereas the invariable plane constant operates in absolute space. To relate these constraints, we note that the gradient vector of the kinetic energy with respect to angular velocity vector equals the angular momentum vector Hence, the normal vector to the kinetic-energy ellipsoid at
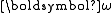isproportional to
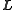, which is also true of the invariable plane.Since their normal vectors point in the same direction, these two surfaces will intersect tangentially.
Taken together, these results show that, in an absolute reference frame, the instantaneous angular velocity vector
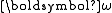is the point of intersection between a fixed invariable plane and a kinetic-energy ellipsoid that is tangent to it and rolls around on it without slipping. This is Poinsot's construction.Derivation of the polhodes in the body frame
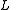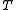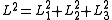
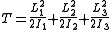
In the principal axis frame (which is rotating in absolute space), the angular momentum vector is not conserved even in the absence of applied torques, but varies as described by Euler's equations. However, in the absence of applied torques, the magnitude of the angular momentum and the kinetic energy are both conservedwhere the
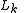are the components of the angular momentum vector along the principal axes, and the 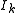are the principal moments of inertia.These conservation laws are equivalent to two constraints to the three-dimensional angular momentum vector
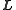.The kinetic energy constrains
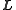to lie on anellipsoid, whereas the angular momentum constraint constrains
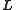to lie on a sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. These two surfaces
intersect in taco-shaped curves that define the possible solutions
for
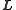.This construction differs from Poinsot's construction because it considers
the angular momentum vector
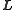rather than the angular velocity vector 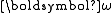. It appears to have been developed by Jacques Philippe Marie BinetJacques Philippe Marie Binet
Jacques Philippe Marie Binet was a French mathematician, physicist and astronomer born in Rennes; he died in Paris, France, in 1856. He made significant contributions to number theory, and the mathematical foundations of matrix algebra which would later lead to important contributions by Cayley...
.
See also
- polhodePolhodeThe details of a spinning body may impose restrictions on the motion of its angular velocity vector, ω. The curve produced by the angular velocity vector on the inertia ellipsoid, is known as the polhode, coined from Greek meaning "path of the pole"...
- precessionPrecessionPrecession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
- Principal axes
- Moment of inertiaMoment of inertiaIn classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
- Tait-Bryan rotations
- Euler anglesEuler anglesThe Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...