
Plücker formula
Encyclopedia
In mathematics
, a Plücker formula, named after Julius Plücker
, is one of a family of formulae, of a type first developed by Plücker in the 1830s, that relate certain numeric invariants of algebraic curve
s to corresponding invariants of their dual curve
s. The invariant called the genus
, common to both the curve and its dual, is connected to the other invariants by similar formulae. These formulae, and the fact that each of the invariants must be a positive integer, place quite strict limitations on their possible values.
. In the correspondence between the projective plane and its dual, points on C correspond to lines tangent C*, so the dual of C* can be identified with C.
The first two invariants covered by the Plücker formulas are the degree d of the curve C and the degree d*, classically called the class of C. Geometrically, d is the number of times a given line intersects C, including complex points and points at infinity, with multiplicities properly counted. Similarly, d* is the number of tangents to C that are lines through a given point on the plane; so for example a conic section
has degree and class both 2. If C has no singularities
, the first Plücker equation states that
but this must be corrected for singular curves.
Of the double points of C, let δ be the number that are ordinary, i.e. that have distinct tangents (these are also called nodes), and let κ be the number that are cusps, i.e. having a single tangent (spinodes). If C has higher order singularities then these are counted as multiple double points according to an analysis of the nature of the singularity. For example an ordinary triple point is counted as 3 double points. Again, complex points and points at infinity are included in these counts. The corrected form is of the first Plücker equation is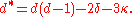
Similarly, let δ* be the number of ordinary double points, and κ* the number of cusps of C*. Then the second Plücker equation states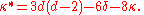
The geometric interpretation of an ordinary double point of C* is a line that is tangent to the curve at two points (double tangent) and the geometric interpretation of a cusp of C* is a point of inflection (stationary tangent).
The first two Plücker equations have dual versions: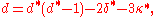
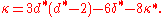
The four equations given so far are, in fact, dependent, so any three may be used to derive the remaining one. From them, given any three of the six invariants, d, d*, δ, δ*, κ, κ*, the remaining three can be computed.
Finally, the genus of C, classically known as the deficiency of C, can be defined as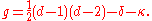
This is equal to the dual quantity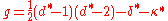
and is a positive integer.
Altogether there are four independent equations in 7 unknowns, and with them any three of these invariants can be used to compute the remaining four.
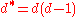
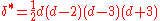
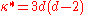
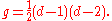
So, for example, a non-singular quartic plane curve
is of genus 3 and has 28 bitangents and 24 points of inflection.
For curves of degree 3 there are three possible types, given by:
Curves of types (ii) and (iii) are the rational cubics and are call nodal and cuspidal respectively. Curves of type {i} are the nonsingular cubics.
For curves of degree 4 there are 10 possible types, given by:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Plücker formula, named after Julius Plücker
Julius Plücker
Julius Plücker was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves.- Early...
, is one of a family of formulae, of a type first developed by Plücker in the 1830s, that relate certain numeric invariants of algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s to corresponding invariants of their dual curve
Dual curve
In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree...
s. The invariant called the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
, common to both the curve and its dual, is connected to the other invariants by similar formulae. These formulae, and the fact that each of the invariants must be a positive integer, place quite strict limitations on their possible values.
Plücker invariants and basic equations
A curve in this context is defined by a non-degenerate algebraic equation in the complex projective plane. Lines in this plane correspond to points in the dual projective plane and the lines tangent to a given algebraic curve C correspond to points in an algebraic curve C* called the dual curveDual curve
In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree...
. In the correspondence between the projective plane and its dual, points on C correspond to lines tangent C*, so the dual of C* can be identified with C.
The first two invariants covered by the Plücker formulas are the degree d of the curve C and the degree d*, classically called the class of C. Geometrically, d is the number of times a given line intersects C, including complex points and points at infinity, with multiplicities properly counted. Similarly, d* is the number of tangents to C that are lines through a given point on the plane; so for example a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
has degree and class both 2. If C has no singularities
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
, the first Plücker equation states that

but this must be corrected for singular curves.
Of the double points of C, let δ be the number that are ordinary, i.e. that have distinct tangents (these are also called nodes), and let κ be the number that are cusps, i.e. having a single tangent (spinodes). If C has higher order singularities then these are counted as multiple double points according to an analysis of the nature of the singularity. For example an ordinary triple point is counted as 3 double points. Again, complex points and points at infinity are included in these counts. The corrected form is of the first Plücker equation is
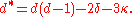
Similarly, let δ* be the number of ordinary double points, and κ* the number of cusps of C*. Then the second Plücker equation states
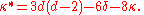
The geometric interpretation of an ordinary double point of C* is a line that is tangent to the curve at two points (double tangent) and the geometric interpretation of a cusp of C* is a point of inflection (stationary tangent).
The first two Plücker equations have dual versions:
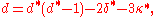
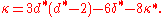
The four equations given so far are, in fact, dependent, so any three may be used to derive the remaining one. From them, given any three of the six invariants, d, d*, δ, δ*, κ, κ*, the remaining three can be computed.
Finally, the genus of C, classically known as the deficiency of C, can be defined as
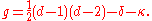
This is equal to the dual quantity
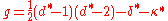
and is a positive integer.
Altogether there are four independent equations in 7 unknowns, and with them any three of these invariants can be used to compute the remaining four.
Non-singular curves
An important special case is when the curve C is non-singular, or equivalently δ and κ are 0, so the remaining invariants can be computed in terms of d only. In this case the results are: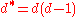
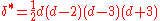
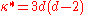
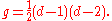
So, for example, a non-singular quartic plane curve
Quartic plane curve
A quartic plane curve is a plane curve of the fourth degree. It can be defined by a quartic equation:Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0....
is of genus 3 and has 28 bitangents and 24 points of inflection.
Curve types
Curves are classified into types according to their Plücker invariants. The Plücker equations together with the restriction that the Plücker invariants must all be natural numbers greatly limits the number of possible types for curves of a given degree. Curves which are projectively equivalent have the same type, though curves of the same type are not, in general, projectively equivalent. Curves of degree 2, conic sections, have a single type given by d=d*=2, δ=δ*=κ=κ*=g=0.For curves of degree 3 there are three possible types, given by:
| Type | d | d* | δ | δ* | κ | κ* | g |
|---|---|---|---|---|---|---|---|
| (i) | 3 | 6 | 0 | 0 | 0 | 9 | 1 |
| (ii) | 3 | 4 | 1 | 0 | 0 | 3 | 0 |
| (iii) | 3 | 3 | 0 | 0 | 1 | 1 | 0 |
Curves of types (ii) and (iii) are the rational cubics and are call nodal and cuspidal respectively. Curves of type {i} are the nonsingular cubics.
For curves of degree 4 there are 10 possible types, given by:
| Type | d | d* | δ | δ* | κ | κ* | g |
|---|---|---|---|---|---|---|---|
| (i) | 4 | 12 | 0 | 28 | 0 | 24 | 3 |
| (ii) | 4 | 10 | 1 | 16 | 0 | 18 | 2 |
| (iii) | 4 | 9 | 0 | 10 | 1 | 16 | 2 |
| (iv) | 4 | 8 | 2 | 8 | 0 | 12 | 1 |
| (v) | 4 | 7 | 1 | 4 | 1 | 10 | 1 |
| (vi) | 4 | 6 | 0 | 1 | 2 | 8 | 1 |
| (vii) | 4 | 6 | 3 | 4 | 0 | 6 | 0 |
| (viii) | 4 | 5 | 2 | 2 | 1 | 4 | 0 |
| (ix) | 4 | 4 | 1 | 1 | 2 | 2 | 0 |
| (x) | 4 | 3 | 0 | 1 | 3 | 0 | 0 |

